2023年12月编程训练
约 2297 个字 684 行代码 预计阅读时间 16 分钟
11. 盛最多水的容器¶
双指针,2023年12月1日
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
示例一
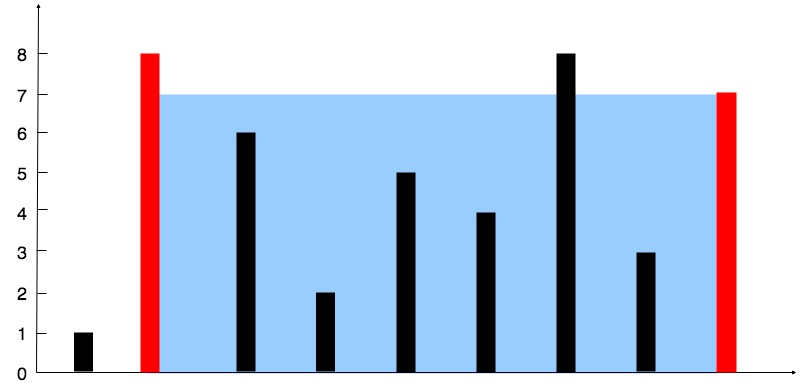
思路¶
在每个状态下,无论长板或短板向中间收窄一格,都会导致水槽 底边宽度 \(−1\) 变短:
- 若向内 移动短板 ,水槽的短板 \(min(h[i],h[j])\) 可能变大,因此下个水槽的面积 可能增大 。
- 若向内 移动长板 ,水槽的短板 \(min(h[i],h[j])\) 不变或变小,因此下个水槽的面积 一定变小 。
因此,初始化双指针分列水槽左右两端,循环每轮将短板向内移动一格,并更新面积最大值,直到两指针相遇时跳出;即可获得最大面积。
class Solution {
public:
int maxArea(vector<int>& h) {
int l = 0,r = h.size() - 1;
int mx = (r - l) * min(h[l],h[r]);
while(l < r) {
if(h[l] < h[r])
l ++;
else r --;
mx = max(mx,(r - l) * min(h[l],h[r]));
}
return mx;
}
};
2661. 找出叠涂元素¶
hash 2023年12月1日
给你一个下标从 0 开始的整数数组 arr 和一个 m x n 的整数 矩阵 mat 。arr 和 mat 都包含范围 [1,m * n] 内的 所有 整数。
从下标 0 开始遍历 arr 中的每个下标 i ,并将包含整数 arr[i] 的 mat 单元格涂色。
请你找出 arr 中在 mat 的某一行或某一列上都被涂色且下标最小的元素,并返回其下标 i 。
示例 1:
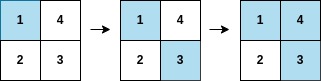
思路¶
1. 记录 mat 矩阵中每一个数的行和列
2. 扫描 arr 数组,每进来一个数,当前的行和列分别加一
3. 当前行/列 满的时候退出
4. 时间复杂度:\(O(n*m) + O(n*m) = O(n*m)\)
class Solution {
public:
int firstCompleteIndex(vector<int>& arr, vector<vector<int>>& mat) {
map<int,pair<int,int>> mp;
int n = mat.size(), m = mat[0].size();
vector<int> row(n,0),col(m,0);
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++) {
mp[mat[i][j]] = {i,j};
}
for(int i = 0; i < n*m; i ++) {
auto [x,y] = mp[arr[i]];
row[x] ++, col[y] ++;
// 注意:某一行有多少个数 = 列的个数
if(row[x] == m || col[y] == n) {
return i;
}
}
return -1; // 实际走不到这里
}
};
238. 除自身以外数组的乘积¶
模拟 2023年12月2日
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
思路¶
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> left(n,1),right(n,1);
// 前缀
for(int i = 1; i < n; i ++)
left[i] = nums[i - 1] * left[i - 1];
// 后缀
for(int j = n-2; j >= 0; j -- )
right[j] = nums[j + 1] * right[j + 1];
// 合并
for(int i = 0; i < n; i ++)
right[i] = left[i] * right[i];
return right;
}
};
1094. 拼车¶
差分数组 2023年12月2日
车上最初有 capacity 个空座位。车 只能 向一个方向行驶(也就是说,不允许掉头或改变方向)
给定整数 capacity 和一个数组 trips , trip[i] = [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客,接他们和放他们的位置分别是 fromi 和 toi 。这些位置是从汽车的初始位置向东的公里数。
当且仅当你可以在所有给定的行程中接送所有乘客时,返回 true,否则请返回 false。
示例 1:
提示:
1 <= trips.length <= 1000trips[i].length == 31 <= numPassengersi <= 1000 <= fromi < toi <= 10001 <= capacity <= 105
思路¶
- 保证,每一站上都是 people < capacity
- 处理差分数组,然后还原数组,某个点上的最大人数
- 一些细节:为了方便,人为规定站点编号从 1 开始。
class Solution {
public:
bool carPooling(vector<vector<int>>& trips, int capacity) {
// 其实用不到排序
/*
auto cmp = [](auto a,auto b) {
if(a[1] == b[1] ) return a[2] < b[2];
return a[1] < b[1];
};
sort(trips.begin(),trips.end(),cmp);
*/
int n = trips.size();
vector<int> peo(1002,0);
for(auto c: trips) {
int from = c[1],to = c[2];
int num = c[0];
peo[from + 1] += num;
peo[to + 1] -= num;
}
for(int i = 1; i <= 1001; i ++) {
peo[i] += peo[i-1];
if(peo[i] > capacity) return false;
}
return true;
}
};
209. 长度最小的子数组¶
模拟 滑动窗口 2023年12月2日
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
提示:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 105
思路¶
第一版代码:
先判断是否有解
有解的话,先找出一个满足条件的解,然后 滑动窗口 (开滑!)
using ll = long long;
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
ll sum = 0;
for(auto c: nums) sum += c;
if(sum < target) return 0;
ll t = 0;
int l = 0,r = 0;
while(t + nums[r] < target) t += nums[r ++];
int res = r - l + 1;
while(r < nums.size()) {
// cout << l << " " << r <<"\n";
t += nums[r++];
while(t >= target) t -= nums[l ++];
res = min(res, r - l + 1);
}
return res;
}
};
第二版代码:
直接滑,满足条件的记录值
using ll = long long;
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
ll sum = 0;
int l = 0,r = 0, res = nums.size() + 1;
while(r < nums.size()) {
sum += nums[r++];
while(sum >= target) {
sum -= nums[l ++];
res = min(res, r - l + 1);
}
}
return res > nums.size() ? 0 : res;
}
};
1423. 可获得的最大点数¶
模拟 滑动窗口 2023年12月3日
几张卡牌 排成一行,每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。
每次行动,你可以从行的开头或者末尾拿一张卡牌,最终你必须正好拿 k 张卡牌。
你的点数就是你拿到手中的所有卡牌的点数之和。
给你一个整数数组 cardPoints 和整数 k,请你返回可以获得的最大点数。
示例 1:
输入:cardPoints = [1,2,3,4,5,6,1], k = 3
输出:12
解释:第一次行动,不管拿哪张牌,你的点数总是 1 。但是,先拿最右边的卡牌将会最大化你的可获得点数。最优策略是拿右边的三张牌,最终点数为 1 + 6 + 5 = 12 。
提示:
1 <= cardPoints.length <= 10^51 <= cardPoints[i] <= 10^41 <= k <= cardPoints.length
思路¶
- 最后的结果:前面 a 个,后面 b 个,a + b = k
- 前假设都在前面选,得到一个
cur结果 - 然后逐次递减在前面选的,从后面选
class Solution {
public:
int maxScore(vector<int>& a, int k) {
// 最后的结果:前面 a 个,后面 b 个,a + b = k
int n = a.size();
int mx = -1,cur = 0;
for(int i = 0; i < k; i ++) cur += a[i];
mx = cur;
// 滑动窗口
for(int l = k-1,r = n - 1; l >= 0; l --,r --) {
cur = cur - a[l] + a[r];
mx = max(mx,cur);
}
return mx;
}
};
1038. 从二叉搜索树到更大和树¶
给定一个二叉搜索树 root (BST),请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
提醒一下, 二叉搜索树 满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例 1:
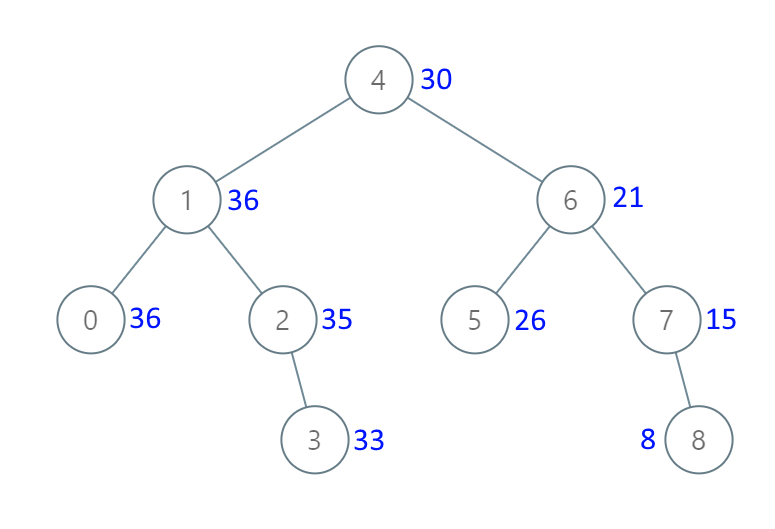
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
提示:
- 树中的节点数在
[1, 100]范围内。 0 <= Node.val <= 100- 树中的所有值均 不重复 。
思路¶
右根左遍历
val 变成在该结点之前访问的 累加值
class Solution {
public:
int sum = 0;
int dfs(TreeNode* root) {
if(!root) return 0;
int r = dfs(root->right);
int val = root->val;
// 遍历右边的值就修改他的值
sum += val;
root->val = sum;
int l = dfs(root->left);
return r + val + l;
}
TreeNode* bstToGst(TreeNode* root) {
dfs(root);
return root;
}
};
1833. 雪糕的最大数量¶
模拟 2023年12月5日
夏日炎炎,小男孩 Tony 想买一些雪糕消消暑。
商店中新到 n 支雪糕,用长度为 n 的数组 costs 表示雪糕的定价,其中 costs[i] 表示第 i 支雪糕的现金价格。Tony 一共有 coins 现金可以用于消费,他想要买尽可能多的雪糕。
注意:Tony 可以按任意顺序购买雪糕。
给你价格数组 costs 和现金量 coins ,请你计算并返回 Tony 用 coins 现金能够买到的雪糕的 最大数量 。
你必须使用计数排序解决此问题。
示例 1:
思路¶
每次选最便宜的买就行了,这样使得剩下钱更多,才可能买更多数量的东西
class Solution {
public:
int maxIceCream(vector<int>& costs, int coins) {
sort(costs.begin(),costs.end());
int res = 0;
for(auto c: costs) {
if(c <= coins) res += 1, coins -= c;
}
return res;
}
};
241. 为运算表达式设计优先级¶
分治 2023年12月6日
给你一个由数字和运算符组成的字符串 expression ,按不同优先级组合数字和运算符,计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。
生成的测试用例满足其对应输出值符合 32 位整数范围,不同结果的数量不超过 104 。
示例 1:
提示:
1 <= expression.length <= 20expression由数字和算符'+'、'-'和'*'组成。- 输入表达式中的所有整数值在范围
[0, 99]
思路¶
不用判断 运算符 的优先级,所以选择 运算符的计算顺序即可
递归出口:纯数字
class Solution {
public:
string s;
vector<int> dfs(int l,int r) {
vector<int> res;
for(int i = l; i <= r; i ++) {
if(s[i] >= '0' && s[i] <= '9') continue;
// 此时 s[i] 是 运算符
// 拿到左边的运算结果,右边的运算结果
// 左边:也是有不同的运算顺序,带来不同的结果
auto left = dfs(l,i-1), right = dfs(i+1,r);
for(int a: left) {
for(int b: right) {
int cur = 0;
if(s[i] == '+') cur = a + b;
else if(s[i] == '-') cur = a - b;
else cur = a * b;
res.push_back(cur);
}
}
}
// 递归出口:纯数字
if(res.empty()) {
int cur = 0;
for(int i = l; i <= r; i ++) cur = cur * 10 + s[i] - '0';
res.push_back(cur);
}
return res;
}
vector<int> diffWaysToCompute(string expression) {
s = expression;
return dfs(0,s.size() - 1);
}
};
1609. 奇偶树¶
dfs 2023年12月7日
如果一棵二叉树满足下述几个条件,则可以称为 奇偶树 :
- 二叉树根节点所在层下标为
0,根的子节点所在层下标为1,根的孙节点所在层下标为2,依此类推。 - 偶数下标 层上的所有节点的值都是 奇 整数,从左到右按顺序 严格递增
- 奇数下标 层上的所有节点的值都是 偶 整数,从左到右按顺序 严格递减
给你二叉树的根节点,如果二叉树为 奇偶树 ,则返回 true ,否则返回 false 。
示例 1:
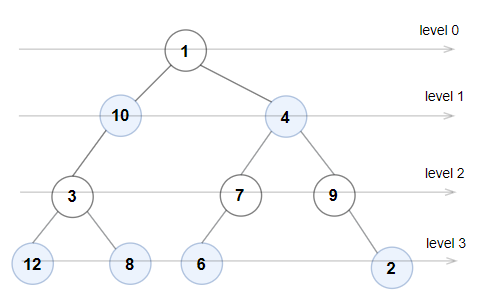
输入:root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
输出:true
解释:每一层的节点值分别是:
0 层:[1]
1 层:[10,4]
2 层:[3,7,9]
3 层:[12,8,6,2]
由于 0 层和 2 层上的节点值都是奇数且严格递增,而 1 层和 3 层上的节点值都是偶数且严格递减,因此这是一棵奇偶树。
提示:
- 树中节点数在范围
[1, 105]内 1 <= Node.val <= 106
思路¶
先判断一下第 \(0\) 层有没有问题
然后 BFS 遍历树,每一层先进去,然后再检查一下是否合规
(这样是为了防止第 \(0\) 层或最后一层没检查到,防止一些 corner case 的情况)
class Solution {
public:
bool isEvenOddTree(TreeNode* root) {
if(root->val % 2 == 0) return false;
// bfs
queue<TreeNode*> q;
q.push(root);
bool even = false;
while(q.size()) {
int n = q.size();
vector<int> level;
for(int i = 0; i < n; i ++) {
auto u = q.front();
q.pop();
if(u->left) {
q.push(u->left);
level.push_back(u->left->val);
}
if(u->right) {
q.push(u->right);
level.push_back(u->right->val);
}
}
// 扫描里面有没有不符合规定的
// 偶数层
if(even) {
int x = -1;
for(auto c: level) {
// 不增 或 偶数
if(c <= x || c%2 == 0) return false;
x = c;
// cout << x << " ";
}
}
else { // 奇数层
int x = 1e7;
for(auto c: level) {
// 不减 或 奇数
if(c >= x || c%2 == 1) return false;
x = c;
// cout << x << " ";
}
}
even = !even;
// cout << "\n";
}
return true;
}
};
1466. 重新规划路线¶
dfs 反向建图 2023年12月7日
n 座城市,从 0 到 n-1 编号,其间共有 n-1 条路线。因此,要想在两座不同城市之间旅行只有唯一一条路线可供选择(路线网形成一颗树)。去年,交通运输部决定重新规划路线,以改变交通拥堵的状况。
路线用 connections 表示,其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。
今年,城市 \(0\) 将会举办一场大型比赛,很多游客都想前往城市 \(0\) 。
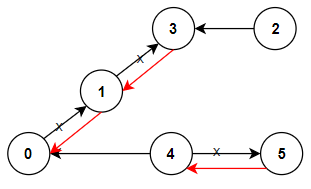
请你帮助重新规划路线方向,使每个城市都可以访问城市 \(0\) 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 \(0\) 。
示例 1:
提示:
2 <= n <= 5 * 10^4connections.length == n-1connections[i].length == 20 <= connections[i][0], connections[i][1] <= n-1connections[i][0] != connections[i][1]
思路¶
核心:先将树转化为dag 有向无环图, 然后再转化为 翻转的根为 \(0\) 的有根树 ,且这种转换 是唯一的 (since 无向图变成有根树每个边的方向就确定了)
原图上从所有点能够访问到 \(0\),等价于反图中从 \(0\) 出发能到任何点。
从 \(0\) 出发: a->b 已经存在边,不存在代价
反过来,从其他点出发:要将a->b 翻转过来,代价为 \(1\)
因此,可用 connections 创建双向图(原边权重为 \(1\),反向边权重为 \(0\)),
然后从 \(0\) 出发访问整张图,统计访问过程中的权重之和,即是原图中需要反向的边的数量。
const int N = 1e5;
class Solution {
public:
// 邻接表
// 反向建图
vector<pair<int,int>> g[N];
int minReorder(int n, vector<vector<int>>& connections) {
for(auto e: connections) {
int a = e[0], b = e[1];
// 从 0 出发: a->b 已经存在边,不存在代价
// 反过来,从其他点出发:要将 a->b 翻转过来,代价为 1
g[a].push_back({b,1});
g[b].push_back({a,0});
}
return dfs(0,-1);
}
int dfs(int u, int fa) {
int res = 0;
for(auto [v,w]: g[u]) {
if(v == fa) continue; // 已经访问过
res += w + dfs(v,u);
}
return res;
}
};
373. 查找和最小的 K 对数字¶
堆 2023年12月8日
给定两个以 非递减顺序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。
定义一对值 (u,v),其中第一个元素来自 nums1,第二个元素来自 nums2 。
请找到和最小的 k 个数对 (u1,v1), (u2,v2) ... (uk,vk) 。
示例 1:
输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数:
[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
提示:
1 <= nums1.length, nums2.length <= 105-109 <= nums1[i], nums2[i] <= 109nums1和nums2均为升序排列1 <= k <= 104
思路¶
令 \(nums1\) 的长度为 \(n\),\(nums2\) 的长度为 \(m\),所有的点对数量为 \(n * m\)。
其中每个 \(nums1[i]\) 参与所组成的点序列为:
由于 \(nums1\) 和 \(nums2\) 均已按升序排序,因此每个 \(nums1[i]\) 参与构成的点序列也为升序排序,这引导我们使用「多路归并」来进行求解。
具体的,起始我们将这 \(n\) 个序列的首位元素(点对)以二元组 \((i, j)\) 放入优先队列(小根堆),其中 \(i\) 为该点对中 \(nums1[i]\) 的下标,\(j\) 为该点对中 \(nums2[j]\) 的下标,这步操作的复杂度为 \(O(n\log{n})\)。这里也可以得出一个小优化是:我们始终确保 \(nums1\) 为两数组中长度较少的那个,然后通过标识位来记录是否发生过交换,确保答案的点顺序的正确性。
每次从优先队列(堆)中取出堆顶元素(含义为当前未被加入到答案的所有点对中的最小值),加入答案,并将该点对所在序列的下一位(如果有)加入优先队列中。
class Solution {
public:
vector<vector<int>> kSmallestPairs(vector<int>& a, vector<int>& b, int k) {
vector<vector<int>> res;
priority_queue<tuple<int,int,int>> q;
// 先让a[0] 和 所有的 b[y] 结合
for(int y = 0; y < b.size(); y ++) {
q.push({-a[0] - b[y],0,y});
}
// 可能会存在不足 k 的时候
while(res.size() < k and q.size()) {
auto [_,x,y] = q.top();
q.pop();
res.push_back({a[x],b[y]});
// 前面是 a[0] + b[y]
// a[1] + b[y + 1]
if(x + 1 < a.size())
q.push({-a[x+1] - b[y], x+1 , y});
}
return res;
}
};
1414. 和为 K 的最少斐波那契数字数目¶
模拟 2023年12月9日
给你数字 k ,请你返回和为 k 的斐波那契数字的最少数目,其中,每个斐波那契数字都可以被使用多次。
斐波那契数字定义为:
- F1 = 1
- F2 = 1
- Fn = Fn-1 + Fn-2 , 其中 n > 2 。
数据保证对于给定的 k ,一定能找到可行解。
示例 1:
思路¶
找出小于 k 的所有 斐波那契数,从大向小遍历
class Solution {
public:
int findMinFibonacciNumbers(int k) {
vector<int> q;
int a = 1, b = 1;
q.push_back(1);
while(b <= k) {
int temp = b;
b = a + b;
a = temp;
q.push_back(b);
}
int n = q.size(),res = 0;
for(int i = n - 1; i >= 1; i --) {
if(k >= q[i]) {
res += 1;
k -= q[i];
cout << q[i] << " ";
}
}
// 剩下的 1 补齐
return res + k;
}
};
70. 爬楼梯¶
线性dp 2023年12月10日
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
思路¶
class Solution {
public:
int climbStairs(int n) {
int a = 1, b = 1, sum;
for(int i = 0; i < n - 1; i++){
sum = a + b;
a = b;
b = sum;
}
return b;
}
};
654. 最大二叉树¶
递归 单调栈 2023年12月11日
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 *最大二叉树* 。
示例 1:

输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
思路¶
递归建树,根节点是区间内的最大值
\(n\) 个点,每个点都要找最大值 ,所以时间复杂度是 \(O(n^2)\)
class Solution {
public:
TreeNode* root = NULL;
vector<int> a;
TreeNode* dfs(int l,int r) {
if(l > r) return NULL;
int mx = -1,u = -1;
for(int i = l; i <= r; i ++) {
if(a[i] > mx) {
mx = a[i];
u = i;
}
}
TreeNode* cur = new TreeNode(a[u]);
cur -> left = dfs(l,u - 1);
cur -> right = dfs(u + 1,r);
return cur;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
a = nums;
return dfs(0,nums.size() - 1);
}
};
单调栈
用std::vector 容器来 维持一个单调递减的栈;
- 当节点值大于栈顶时,弹出栈顶作为当前节点的左孩子(可以理解为维护不了单调栈了要弹出,比当前节点这个较大值更早出现,因此在左边
- 栈顶的右孩子就是当前节点(比栈顶晚出现,就在其右边
- 当前节点加入栈
- 举例子 `nums = [3,2,1,6,0,5]`
- 构造节点3,初始栈为空,节点3入栈
- 构造节点2,栈顶3大于2,栈顶节点3的右孩子是当前节点2,节点2入栈
- 构造节点1,栈顶2大于1,栈顶节点2的右孩子是当前节点1,节点1入栈
- 构造节点6,栈顶1小于6,弹出栈顶,节点6的左孩子是栈顶1,节点2和3依次被弹出,都是6的左孩子,栈空,节点6入栈
- 构造节点0,栈顶6大于1,栈顶节点6的右孩子是当前节点0,节点0入栈
- 构造节点5,栈顶0小于5,弹出栈顶,节点5的左孩子是栈顶0;栈顶节点6的右孩子是当前节点5,节点5入栈
- 返回栈底元素6就是根节点
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
std::vector<TreeNode*> stk(1010, nullptr);
int l = 0, r = 0;
for (int x : nums) {
TreeNode* node = new TreeNode(x);
// 找到比当前结点小的结点中最大的一个
while (l < r && stk[r - 1]->val < x)
node->left = stk[--r];
// 右边结点的左边的最大一个就是 node
if (l < r)
stk[r - 1]->right = node;
stk[r++] = node;
}
return stk[0];
}
};
109. 有序链表转换二叉搜索树¶
dfs 2023年12月12日
给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为高度平衡的二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。
示例 1:
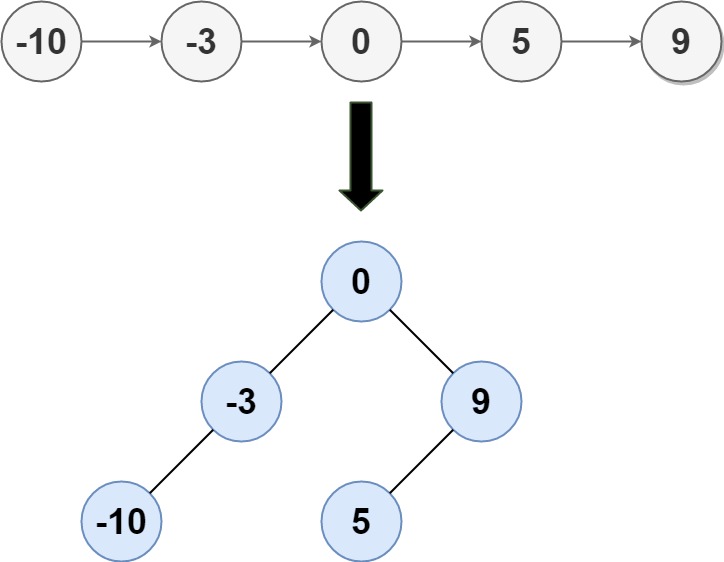
思路¶
构造一颗二叉判定树即可,二叉判定树就是平衡树。
class Solution {
public:
TreeNode* sortedListToBST(ListNode* head) {
int n = 0;
ListNode* cur = head;
while(cur) {
cur = cur -> next;
n ++;
}
return build(head, 0, n - 1);
}
TreeNode* build(ListNode* head, int l, int r) {
if (l > r) return nullptr;
int mid = l + r >> 1, t = mid - l;
ListNode* cur = head;
while (t-- > 0) cur = cur->next;
TreeNode* ans = new TreeNode(cur->val);
ans->left = build(head, l, mid - 1);
ans->right = build(cur->next, mid + 1, r);
return ans;
}
};
96. 不同的二叉搜索树¶
线性dp 2023年12月13日
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
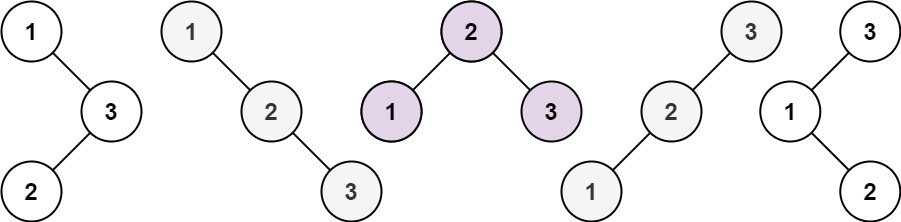
思路¶
考虑第三棵树是如何构建的
- 第三颗树 一定是由左子树和右子树构成的
- 左子树的结点个数 是从 \(0\) 到 \(i-1\) , 对应的 右子树的结点 是 \(i-1\) 到 \(0\)
- 结点个数确定之后,下面讨论 整棵树 有多少种
令 f[i] 表示 由 \(i\) 个结点组成二叉搜索树 的种类数目
由上面的讨论可以得到 f[i] 是由两个 子树构成的,
左子树的种类数目 * 右子树的种类数目 ==》 这种形状 的 二叉搜索树的 种类数目
总结点数是确定的,循环左子树结点个数即可
class Solution {
public:
int f[20];
int numTrees(int n) {
f[0] = 1,f[1] = 1,f[2] = 2;
for(int i = 3; i <= n; i ++)
for(int j = 0; j < i; j ++)
f[i] += f[j] * f[i-1-j];
return f[n];
}
};
LCR 151. 彩灯装饰记录 III¶
bfs 层序遍历 2023年12月14日
一棵圣诞树记作根节点为 root 的二叉树,节点值为该位置装饰彩灯的颜色编号。请按照如下规则记录彩灯装饰结果:
- 第一层按照从左到右的顺序记录
- 除第一层外每一层的记录顺序均与上一层相反。即第一层为从左到右,第二层为从右到左。
示例 1:

思路¶
层序遍历,偶数层翻转输出结果
class Solution {
public:
vector<vector<int>> decorateRecord(TreeNode* root) {
vector<vector<int>> res;
if(!root) return res;
// 层序遍历
queue<TreeNode*> q;
vector<int> level;
level.push_back(root->val);
q.push(root);
res.push_back(level);
bool f = true;
while(q.size()) {
int n = q.size();
level.clear();
while(n-- > 0) {
auto x = q.front();
q.pop();
if(x->left) {
q.push(x->left);
level.push_back(x->left->val);
}
if(x->right) {
q.push(x->right);
level.push_back(x->right->val);
}
}
if(f) {
reverse(level.begin(),level.end());
}
f = !f;
if(level.size()) res.push_back(level);
}
return res;
}
};
916. 单词子集¶
模拟 2023年12月14日
给你两个字符串数组 words1 和 words2。
现在,如果 b 中的每个字母都出现在 a 中,包括重复出现的字母,那么称字符串 b 是字符串 a 的 子集 。
- 例如,
"wrr"是"warrior"的子集,但不是"world"的子集。
如果对 words2 中的每一个单词 b,b 都是 a 的子集,那么我们称 words1 中的单词 a 是 通用单词 。
以数组形式返回 words1 中所有的通用单词。你可以按 任意顺序 返回答案。
示例 1:
输入:words1 = ["amazon","apple","facebook","google","leetcode"], words2 = ["e","oo"]
输出:["facebook","google"]
思路¶
存储 words2 中出现的所有字母和 最大 频数,然后在 words1中查
temp.clear(); :clear 只会将 temp.size() 置为零,值不变,没有释放内存空间
class Solution {
public:
vector<string> wordSubsets(vector<string>& words1, vector<string>& words2) {
// 存储 words2 中出现的所有字母和 最大 频数,然后在 words1 中查
vector<int> st(27,0),temp(27,0);
for(auto word: words2) {
// temp.clear(); clear 只会将 temp.size() 置为零,值不变,没有释放内存空间
temp = vector<int>(27,0);
for(auto c: word) {
temp[c - 'a'] ++;
}
for(int i = 0; i < 26; i ++) st[i] = max(st[i],temp[i]);
}
vector<string> res;
for(auto word: words1) {
temp = vector<int>(27,0);
for(auto c: word) {
temp[c - 'a'] ++;
}
bool f = true;
for(int i = 0; i < 26; i ++) {
if(temp[i] < st[i]) f = false;
}
if(f) res.push_back(word);
}
return res;
}
};
200. 岛屿数量¶
dfs 连通块 2023年12月15日
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 :
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]的值为'0'或'1'
思路¶
考虑有多少个连通块
const int N = 310;
class Solution {
public:
bool st[N][N] = {0};
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
int n,m;
vector<vector<char>> g;
void dfs(int i,int j) {
st[i][j] = true;
for(int k = 0; k < 4; k ++) {
int x = i + dx[k],y = j + dy[k];
if(x < 0 || x >= m || y < 0 || y >= n) continue;
if(st[x][y] || g[x][y] == '0') continue;
dfs(x,y);
}
}
int numIslands(vector<vector<char>>& grid) {
int cnt = 0;
m = grid.size(), n = grid[0].size();
g = grid;
for(int i = 0; i < m; i ++)
for(int j = 0; j < n; j ++)
if(!st[i][j] && grid[i][j] == '1')
{
dfs(i,j);
cnt ++;
}
return cnt;
}
};
313. 超级丑数¶
质因数 多路归并 2023年12月16日
超级丑数 是一个正整数,并满足其所有质因数都出现在质数数组 primes 中。
给你一个整数 n 和一个整数数组 primes ,返回第 n 个 超级丑数 。
题目数据保证第 n 个 超级丑数 在 32-bit 带符号整数范围内。
示例 1:
输入:n = 12, primes = [2,7,13,19]
输出:32
解释:给定长度为 4 的质数数组 primes = [2,7,13,19],前 12 个超级丑数序列为:[1,2,4,7,8,13,14,16,19,26,28,32] 。
提示:
1 <= n <= 1051 <= primes.length <= 1002 <= primes[i] <= 1000- 题目数据 保证
primes[i]是一个质数 primes中的所有值都 互不相同 ,且按 递增顺序 排列
思路¶
根据丑数的定义,我们有如下结论:
- \(1\) 是最小的丑数。
- 对于任意一个丑数 \(x\),其与任意给定的质因数
primes[i]相乘,结果仍为丑数。
利用题目规定的答案为 int 范围,以及丑数性质,我们可以直接在入队的时候做控制。
class Solution {
public:
int nthSuperUglyNumber(int n, vector<int>& primes) {
priority_queue<long,vector<long>,greater<long>> q;
q.push(1);
int x;
for(int i = 0; i < n; i ++) {
x = q.top();
q.pop();
for(int c: primes) {
if(c <= INT_MAX / x) q.push(c * x);
if(x % c == 0) break;
}
}
return x;
}
};
746. 使用最小花费爬楼梯¶
线性dp 2023年12月17日
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
提示:
2 <= cost.length <= 10000 <= cost[i] <= 999
思路¶
注意,结束的时候是登上第 \(n\) 层 (\(0\) base)
登上第三层:第零层 + cost[0] , 第一层 + cost[0],两者取最小值
初始 dp[0] = dp[1] = 0 , 初始地可以不用花费代价。
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> dp(n+10,0);
dp[0] = dp[1] = 0;
for(int i = 2; i <= n; i ++) {
dp[i] = min(dp[i-1] + cost[i-1],dp[i-2] + cost[i-2]);
}
return dp[n];
}
};
319. 灯泡开关¶
数论 2023年12月18日
初始时有 n 个灯泡处于关闭状态。第一轮,你将会打开所有灯泡。接下来的第二轮,你将会每两个灯泡关闭第二个。
第三轮,你每三个灯泡就切换第三个灯泡的开关(即,打开变关闭,关闭变打开)。第 i 轮,你每 i 个灯泡就切换第 i 个灯泡的开关。直到第 n 轮,你只需要切换最后一个灯泡的开关。
找出并返回 n 轮后有多少个亮着的灯泡。
思路¶
经过 \(n\) 轮,第 \(i\) 个灯泡被操作了奇数次还是偶数次?
奇数次则最后是亮的,偶数次则最后是关闭的。
什么数的因数的个数是奇数个?
答案是完全平方数。
证明过程:
设 \(P,A,B\) 为正整数,如果 \(P=A*B\),则 \(A\) 和 \(B\) 为 \(P\) 的因数。 \(P\) 的因数 \(A\) 和 \(B\) 总是成对出现。也就是说他们总是一起为 \(P\) 的因数个数做贡献。但是如果他们相等呢?这个时候他们一起只会为因数的个数贡献 \(1\)。
其次,\(P=A*A\),这种情况对于 \(P\) 来说最多只能出现 \(1\) 次,而这种情况只可能出现在完全平方数中。
所以对于正整数而言,只有完全平方数的因数的个数是奇数个。
综上所述,所以每个完全平方数就是答案
数学推导
- 对于数 \(k\),第 \(i\) 轮被拨一下的条件是 \(k%i==0\)
- 所有数 \(k\) 被拨的次数是 \(k\) 的约束的个数
- 若 \(k=p_1^x p_2^y p_3^z ...\) , 其中 \(p_i\) 为素数,则约数的个数 \(f(k)= (1+x)(1+y)(1+z)\).
- 第 \(k\) 个灯亮意味着 \(f(k)\) 为奇数,根据推论 \(3\) 可知,其中的 \(x,y,z...\) 都必须为偶数。
- 回看,$k=p_1^x p_2^y p_3^z ... $, 说明 \(k\)是个完全平方数
1901. 寻找峰值 II¶
模拟 2023年12月19日
一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。
给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。
你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。
要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法
示例 1:
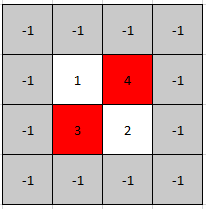
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 5001 <= mat[i][j] <= 105- 任意两个相邻元素均不相等.
思路¶
class Solution {
public:
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
vector<int> findPeakGrid(vector<vector<int>>& a) {
int n = a.size(), m = a[0].size();
for(int i = 0; i < n; i ++) {
for(int j = 0; j < m; j ++) {
bool f = true;
for(int k = 0; k < 4; k ++) {
int x = i + dx[k], y = j + dy[k];
if(x < 0 || x >= n || y < 0 || y >= m) continue;
if(a[i][j] <= a[x][y]) f = false;
}
if(f) {
return {i,j};
}
}
}
return {-1,-1};
}
};
1276. 不浪费原料的汉堡制作方案¶
模拟 2023年12月25日
圣诞活动预热开始啦,汉堡店推出了全新的汉堡套餐。为了避免浪费原料,请你帮他们制定合适的制作计划。
给你两个整数 tomatoSlices 和 cheeseSlices,分别表示番茄片和奶酪片的数目。不同汉堡的原料搭配如下:
- 巨无霸汉堡:4 片番茄和 1 片奶酪
- 小皇堡:2 片番茄和 1 片奶酪
请你以 [total_jumbo, total_small]([巨无霸汉堡总数,小皇堡总数])的格式返回恰当的制作方案,使得剩下的番茄片 tomatoSlices 和奶酪片 cheeseSlices 的数量都是 0。
如果无法使剩下的番茄片 tomatoSlices 和奶酪片 cheeseSlices 的数量为 0,就请返回 []。
示例 1:
输入:tomatoSlices = 16, cheeseSlices = 7
输出:[1,6]
解释:制作 1 个巨无霸汉堡和 6 个小皇堡需要 4*1 + 2*6 = 16 片番茄和 1 + 6 = 7 片奶酪。不会剩下原料。
提示:
0 <= tomatoSlices <= 10^70 <= cheeseSlices <= 10^7
思路¶
class Solution {
public:
vector<int> numOfBurgers(int tomatoSlices, int cheeseSlices) {
// 4x + 2y = tomatoSlices
// 2x + 2y = 2cheeseSlices
// x >= 0, y >= 0
if((tomatoSlices - 2*cheeseSlices) % 2 == 0 && tomatoSlices - 2*cheeseSlices >= 0) {
int x = (tomatoSlices - 2*cheeseSlices) / 2;
if(cheeseSlices - x >= 0)
return {x,cheeseSlices - x};
}
return {};
}
};
Created: December 1, 2023