2023年04月编程训练
831. 隐藏个人信息¶
模拟 2023年4月1日
字符串模拟题。
代码
class Solution {
public:
string maskPII(string s) {
bool email = false;
string ss;
for(int i=0;i<s.size();i++)
{
if(s[i]=='@') {
email = true;
ss=s.substr(0,i);
}
}
string res = "";
if(email){
res += tolower(ss[0]);
res += "*****";
res += tolower(ss[ss.size()-1]);
bool f = false;
for(auto c:s) {
if(f) {
res += tolower(c);
}else if(c=='@'){
f = true;
res += c;
}
}
}
else {
vector<char> t;
for(auto c:s) {
if(isdigit(c)) {
t.push_back(c);
}
}
if(t.size()==10) {
res += "***-***-";
}else {
res += '+';
for(int i = t.size()-11;i>=0;i--) {
res += '*';
}
res += "-***-***-";
}
for(int i = t.size()-4,cnt = 0; cnt < 4 ;cnt ++,i ++){
res += t[i];
}
}
return res;
}
};
417. 太平洋大西洋水流问题¶
dfs 2023年4月2日
思路:分别从与当前海域直接相连的边缘格子出发,统计能够流向当前海域的格子集合,两片海域求得的集合交集即是答案。
代码
class Solution {
public:
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
vector<vector<int>> pacificAtlantic(vector<vector<int>>& a) {
int n = a.size();
int m = a[0].size();
vector<vector<int>> ans;
bool st[2][n][m];
memset(st,0,sizeof st);
function<void(int,int,bool)> dfs = [&](int i,int j,bool op) -> void {
if(st[op][i][j]) return;
st[op][i][j] = true;
for(int k = 0; k < 4; k ++ ) {
int x = i + dx[k], y = j + dy[k];
if(x<0 || x>=n || y<0 || y>=m) continue;
if(a[x][y] < a[i][j]) continue;
dfs(x,y,op);
}
return;
};
for(int j = 0; j < m; j ++ ) {
dfs(n-1,j,0);
dfs(0,j,1);
}
for(int i = 0; i < n; i ++ ) {
dfs(i,m-1,0);
dfs(i,0,1);
}
for(int i = 0; i < n; i ++ ) {
for(int j = 0; j < m; j ++ ){
if(st[0][i][j] and st[1][i][j]) {
ans.push_back({i,j});
}
}
}
return ans;
}
};
443. 压缩字符串¶
模拟 2023年4月2日
字符串模拟题:存储最后一个字母且记录字符的个数。
代码
1039. 多边形三角剖分的最低得分¶
区间dp 记忆化搜索 2023年4月2日
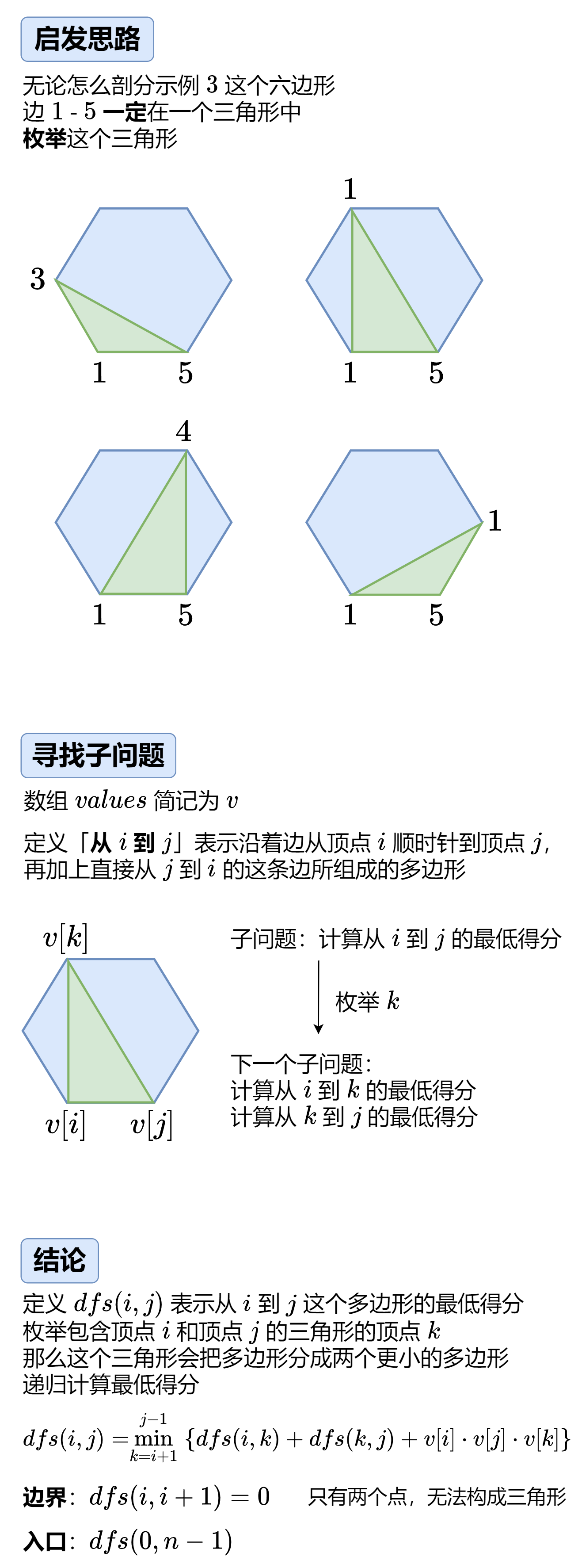
代码
class Solution {
public:
int minScoreTriangulation(vector<int>& v) {
int n = v.size();
int f[n][n];
memset(f,255,sizeof f);
function<int(int,int)> dfs = [&](int i,int j) -> int {
if(i + 1 == j) return 0;
if(f[i][j] != -1) return f[i][j];
int res = INT_MAX;
for(int k = i + 1; k < j; k ++ ) {
res = min(res,dfs(i,k) + dfs(k,j) + v[i]*v[j]*v[k]);
}
return f[i][j] = res;
};
return dfs(0,n-1);
}
};
127. 单词接龙¶
bfs 双向bfs 2023年4月3日
普通 BFS 写法,
从 beginWord 出发,枚举所有替换一个字符的方案,如果方案存在于 wordList 中,则加入队列中,这样队列中就存在所有替换次数为 111 的单词。然后从队列中取出元素,继续这个过程,直到遇到 endWord 或者队列为空为止。
当枚举到新单词 str 时,需要先检查是否已经存在与「哈希表」中,如果不存在则更新「哈希表」并将新单词放入队列中。
代码
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
unordered_map<string,int> mp;
queue<string> q;
q.push(beginWord);
mp[beginWord] = 1;
set<string> list;
for(auto c:wordList) list.insert(c);
while(q.size()) {
auto c = q.front();
q.pop();
for(char &v:c) {
char t = v;
string s = c;
for(char i = 'a'; i <= 'z'; i ++ ) {
v = i;
if(!mp.count(c) && list.count(c)) {
mp[c] = mp[s] + 1;
q.push(c);
if(c == endWord) return mp[c];
}
v = t;
}
}
}
return mp[endWord];
}
};
「双向 BFS」 的基本实现思路如下:
- 创建「两个队列」分别用于两个方向的搜索;
- 创建「两个哈希表」用于「解决相同节点重复搜索」和「记录转换次数」;
- 为了尽可能让两个搜索方向“平均”,每次从队列中取值进行扩展时,先判断哪个队列容量较少;
- 如果在搜索过程中「搜索到对方搜索过的节点」,说明找到了最短路径。
「双向 BFS」基本思路对应的伪代码大致如下:
d1、d2 为两个方向的队列
m1、m2 为两个方向的哈希表,记录每个节点距离起点的
// 只有两个队列都不空,才有必要继续往下搜索
// 如果其中一个队列空了,说明从某个方向搜到底都搜不到该方向的目标节点
while(d1.size() && d2.size()) {
if (d1.size() < d2.size()) {
update(d1, m1, m2);
} else {
update(d2, m2, m1);
}
}
// update 为将当前队列 d 中包含的元素取出,进行「一次完整扩展」的逻辑(按层拓展)
void update(Deque d, Map cur, Map other) {}
代码
```c++
class Solution {
public:
set
int update(queue<string>& q,unordered_map<string,int>& cur,unordered_map<string,int>& other) {
int n = q.size();
while(n-- > 0) {
string ss = q.front();
q.pop();
string s = ss;
for(char& v : s) {
char t = v;
for(char c = 'a'; c <= 'z'; c ++ ) {
v = c;
if(list.count(s)) {
if(cur.count(s)) {
v = t;
continue;
}
if(other.count(s))
return cur[ss] + 1 + other[s] ;
else {
q.push(s);
cur[s] = cur[ss] + 1;
}
}
v = t;
}
}
}
return -1;
}
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
list.clear();
for(auto c:wordList) list.insert(c);
if(list.count(endWord) == 0) return 0;
// 双向BFS
queue<string> d1,d2;
unordered_map<string,int> m1,m2;
d1.push(beginWord);
m1[beginWord] = 0;
d2.push(endWord);
m2[endWord] = 0;
while(d1.size() and d2.size()) {
// 为了让两个方向的搜索尽可能平均,优先拓展队列内元素少的方向
int t = -1;
if(d1.size() <= d2.size())
t = update(d1,m1,m2);
else
t = update(d2,m2,m1);
if(t != -1) return t + 1;
}
return 0;
}
};
```
752. 打开转盘锁¶
双向bfs 2023年4月3日
注意边界情况。
可以直接复制一个串,在 copy 串上做修改,防止做修改没改回去导致一直 wa
代码
```c++
class Solution {
public:
set
while(q1.size() and q2.size()) {
int t = -1;
if(q1.size() <= q2.size())
t = update(q1,m1,m2);
else
t = update(q2,m2,m1);
if(t != -1) {
return t;
}
}
return -1;
}
int update(queue<string> &q,unordered_map<string,int>& cur,unordered_map<string,int>& other) {
int n = q.size();
while(n--) {
auto s = q.front();
q.pop();
string ss = s;
for(char & v:s) {
char c = v;
for(int i = -1; i <= 1; i ++) {
if(i == 0) continue;
int p = v - '0';
p = (p + i + 10)% 10;
v = '0' + p;
if(ban.count(s) || cur.count(s)) {
v = c;
continue;
}
if(other.count(s))
return cur[ss] + 1 + other[s];
else {
q.push(s);
cur[s] = cur[ss] + 1;
}
v = c;
}
}
}
return -1;
}
};
```
31. 下一个排列¶
模拟 2023年4月3日
代码
1053. 交换一次的先前排列¶
模拟 2023年4月3日
代码
1162. 地图分析¶
多源bfs 2023年4月5日
多源最短路与「单源最短路」不同,「多源最短路」问题是求从「多个源点」到达「一个/多个汇点」的最短路径。
在实现上,最核心的搜索部分,「多源 BFS」与「单源 BFS」并无区别。
并且通过建立 「虚拟源点」 的方式,我们可以「多源 BFS」转换回「单源 BFS」问题。
在这个题中,我们可以将「源点/起点」和「汇点/终点」进行反转:从每个「陆地」区域出发,多个「陆地」区域每次同时向往扩散一圈,每个「海洋」区域被首次覆盖时所对应的圈数,就是「海洋」区域距离最近的「陆地」区域的距离。
代码
class Solution {
public:
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
int maxDistance(vector<vector<int>>& g) {
int n = g.size(), m = g[0].size();
vector<vector<int>> dis(n,vector<int>(m,0x3f3f3f3f));
// 多源BFS
queue<pair<int,int>> q;
for(int i = 0; i < n; i ++ )
for(int j = 0; j < m; j ++ )
if(g[i][j] == 1) {
dis[i][j] = 0;
q.push({i,j});
}
while(q.size())
{
auto [x,y] = q.front();
q.pop();
for(int i = 0; i < 4; i ++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if(dis[nx][ny] == 0x3f3f3f3f) {
dis[nx][ny] = dis[x][y] + 1;
q.push({nx,ny});
}
}
}
int ans = -1;
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
if(g[i][j] == 0)
ans = max(ans,dis[i][j]);
return ans == 0x3f3f3f3f? -1: ans;
}
};
1765. 地图中的最高点¶
多源bfs 2023年4月5日
代码
class Solution {
public:
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
vector<vector<int>> highestPeak(vector<vector<int>>& g) {
int n = g.size() , m = g[0].size();
// 多源 BFS
queue<pair<int,int>> q;
vector<vector<int>> dis(n,vector<int>(m,0x3f3f3f3f));
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
if(g[i][j]) {
dis[i][j] = 0;
q.emplace(i,j);
}
while(q.size()) {
auto [x,y] = q.front();
q.pop();
for(int i = 0; i < 4; i ++)
{
int nx = x + dx[i] , ny = y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if(dis[nx][ny] == 0x3f3f3f3f) {
dis[nx][ny] = dis[x][y] + 1;
q.emplace(nx,ny);
}
}
}
return dis;
}
};
2427. 公因子的数目¶
模拟 2023年4月5日
代码
2059. 转化数字的最小运算数¶
双向bfs 2023年4月6日
代码
using ll = long long ;
class Solution {
public:
int target ;
int minimumOperations(vector<int>& nums, int start, int goal) {
target = goal;
queue<ll> q1,q2;
unordered_map<ll,int> m1,m2;
q1.emplace(start);
m1[start] = 0;
q2.emplace(goal);
m2[goal] = 0;
while(q1.size() and q2.size())
{
int t = -1;
if(q1.size() <= q2.size())
t = update(nums,q1,m1,m2);
else
t = update(nums,q2,m2,m1);
if(t != -1) return t;
}
return -1;
}
int update(vector<int>& nums,queue<ll>& q,unordered_map<ll,int>& cur,unordered_map<ll,int>& other)
{
int n = q.size();
while(n--)
{
int x = q.front();
q.pop();
for(auto c:nums) {
ll t ;
t = x + c;
if(!cur.count(t)) {
if(other.count(t)) return cur[x] + 1 + other[t];
else {
if(t>=0 and t <= 1000)
{
q.emplace(t);
cur[t] = cur[x] + 1;
}
}
}
t = x - c;
if(!cur.count(t)) {
if(other.count(t)) return cur[x] + 1 + other[t];
else {
if(t>=0 and t <= 1000)
{
q.emplace(t);
cur[t] = cur[x] + 1;
}
}
}
t = x ^ c;
if(!cur.count(t)) {
if(other.count(t)) return cur[x] + 1 + other[t];
else {
if(t>=0 and t <= 1000)
{
q.emplace(t);
cur[t] = cur[x] + 1;
}
}
}
}
}
return -1;
}
};
433. 最小基因变化¶
bfs 2023年4月7日
代码
class Solution {
public:
int minMutation(string startGene, string endGene, vector<string>& bank) {
queue<string> q;
unordered_map<string,int> mp;
q.emplace(startGene);
mp[startGene] = 0;
unordered_map<string,int> st;
for(auto c:bank) st[c] = 1;
st[startGene] = 1;
if(!st.count(endGene)) return -1;
char a[4] = {'A','C','G','T'};
while(q.size())
{
auto x = q.front();
q.pop();
if(x == endGene) return mp[x];
for(int i = 0; i < x.size(); i ++)
{
auto copy = x;
for(int j = 0; j < 4; j ++)
{
copy[i] = a[j];
// cout << copy << "\n";
if(st.count(copy) && !mp.count(copy)) {
mp[copy] = mp[x] + 1;
q.emplace(copy);
}
}
}
}
return -1;
}
};
1770. 执行乘法运算的最大分数¶
dp 记忆化搜索 2023年4月7日
给你两个长度分别 n 和 m 的整数数组 nums 和 multipliers ,其中 n >= m ,数组下标 从 1 开始 计数。
初始时,你的分数为 0 。你需要执行恰好 m 步操作。在第 i 步操作(从 1 开始 计数)中,需要:
- 选择数组
nums开头处或者末尾处 的整数x。 - 你获得
multipliers[i] * x分,并累加到你的分数中。 - 将
x从数组nums中移除。
在执行 m 步操作后,返回 最大 分数。
数据范围:
n == nums.lengthm == multipliers.length1 <= m <= 103m <= n <= 105-1000 <= nums[i], multipliers[i] <= 1000
输入输出
输入:nums = [1,2,3], multipliers = [3,2,1]
输出:14
输入:nums = [-5,-3,-3,-2,7,1], multipliers = [-10,-5,3,4,6]
输出:102
思路¶
很显然需要用到 dp , 在这里我们定义 f[i][l] 为 第 \(i\) 次操作且开头处为 \(j\) 的最大分数。
这样定义的目的是因为 \(n <= 1e5\),显然不能开 f[n][n],否则内存爆炸
进行 \(m\) 次操作,每次操作有两种选择:用开头处元素表示
- 在第 \(i\) 次操作中,此时数组为
[l,r] - 若选择开头处,则
f[i][l+1] - 若选择结尾处,则
f[i][l] - 两者不同,且唯一区分
代码
class Solution {
public:
int maximumScore(vector<int>& a, vector<int>& mul) {
int n = a.size() , m = mul.size();
vector< vector<int> > f(m,vector<int>(m,0));
function<int(int,int,int)> dfs = [&](int i,int l,int r) -> int{
if(i == m) return 0;
if(f[i][l] != 0) return f[i][l];
int res1 = a[l] * mul[i] + dfs(i + 1, l + 1, r);
int res2 = a[r] * mul[i] + dfs(i + 1, l, r - 1);
return f[i][l] = max(res1,res2);
};
return dfs(0,0,n-1);
}
};
Py
class Solution:
def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:
n = len(multipliers)
@cache
def dfs(idx, l, r):
if idx == n:
return 0
res1 = multipliers[idx] * nums[l] + dfs(idx+1, l+1, r)
res2 = multipliers[idx] * nums[r] + dfs(idx+1, l, r-1)
return max(res1,res2)
return dfs(0,0,len(nums)-1)
1771. 由子序列构造的最长回文串的长度¶
dp 2023年4月7日
给你两个字符串 word1 和 word2 ,请你按下述方法构造一个字符串:
- 从
word1中选出某个 非空 子序列subsequence1。 - 从
word2中选出某个 非空 子序列subsequence2。 - 连接两个子序列
subsequence1 + subsequence2,得到字符串。
返回可按上述方法构造的最长 回文串 的 长度 。如果无法构造回文串,返回 0 。
字符串 s 的一个 子序列 是通过从 s 中删除一些(也可能不删除)字符而不更改其余字符的顺序生成的字符串。
回文串 是正着读和反着读结果一致的字符串。
数据范围:
1 <= word1.length, word2.length <= 1000word1和word2由小写英文字母组成
输入输出
输入:word1 = "cacb", word2 = "cbba"
输出:5
输入:word1 = "ab", word2 = "ab"
输出:3
输入:word1 = "aa", word2 = "bb"
输出:0
思路¶
由于题目限制 word2 子串拼接在 word1 子串的后面,因此可以先将两个字符串拼接成一个大字符串word = word1 + word2,而后即可转化成对s 求解最长回文子串问题。
首先定义状态:f[i][j]表示在 s 中,以下标 \(i\) 起始到下标 \(j\) 结尾的连续子串中,最长回文子串的长度。
故可以根据s[i] s[j]是否相等进行状态转移: 写出状态转移方程:
s[i] == s[j] : f[i][j] = f[i+1][j-1] + 2;s[i] != s[j] : f[i][j] = max(f[i][j-1], f[i+1][j]);
更新 ans 时需要保证 \(i\) 和 \(j\) 两个下标分别属于 word1 和 word2 两段。
代码
class Solution {
public:
int longestPalindrome(string word1, string word2) {
string s = word1 + word2;
int n = s.size();
vector< vector<int> > f(n, vector<int>(n,0));
int ans = 0;
for(int len = 1; len <= n; len ++) {
for(int l = 0; l + len <= n; l ++) {
int r = l + len - 1;
if(len == 1)
f[l][r] = 1;
else {
f[l][r] = max(f[l+1][r] , f[l][r-1]);
if(s[l] == s[r]) {
f[l][r] = f[l+1][r-1] + 2;
if(l < word1.size() and word1.size() <= r)
ans = max(ans, f[l][r]);
}
}
}
}
return ans;
}
};
DFS递归 + 位图¶
2023年4月8日
0/1背包问题
看了下数据量, \(arr.length <= 16, arr[i].length <= 26\),如果直接DFS递归,$ 2^n * arr[i].length = 2^{16} * 26$
粗略算下,64*1000*26,数量级:\(10^6\),小于\(10^8\),可以跑过,不会超时,直接DFS递归完事。
时间:\(O(2^n * m)\),\(其中n: arr长度,m:字符串平均长度;\)
class Solution {
public:
int maxLength(vector<string>& arr) {
int ans = 0;
int n = arr.size();
function<void(int,int,int)> dfs = [&](int u,int len,int mask) -> void {
if(u == n) {
ans = max(len,ans);
return;
}
// 不选第 u 个
dfs(u + 1, len, mask);
for(char c:arr[u]) {
int idx = c - 'a';
if(((mask >> idx) & 1) == 1) return;
mask |= (1 << idx);
}
// 选第 u 个
dfs(u + 1, len + arr[u].size(), mask);
};
dfs(0,0,0);
return ans;
}
};
773. 滑动谜题¶
bfs 2023年4月8日
将二维的图转化为一维的字符串
每次修改直接在字符串上进行修改
然后就是 BFS 求最短路了捏
代码
class Solution {
public:
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
struct Node {
string str;
int x, y;
Node(string _str, int _x, int _y) {
str = _str; x = _x; y = _y;
}
};
int slidingPuzzle(vector<vector<int>>& g) {
int sx,sy;
for(int i = 0; i < 2; i ++)
for(int j = 0; j < 3; j ++)
if(g[i][j] == 0)
sx = i, sy = j;
string start = "";
for(int i = 0; i < 2; i ++)
for(int j = 0; j < 3; j ++)
start.push_back(g[i][j] + '0');
auto update = [](string old,int tx,int ty,int x,int y) -> string {
swap(old[tx*3 + ty],old[x*3 + y]);
return old;
};
//bfs
queue< Node > q;
unordered_map<string,int> mp;
mp[start] = 0;
string end = "123450";
q.emplace(start,sx,sy);
while(q.size())
{
auto [old,x,y] = q.front();
q.pop();
if(old == end) return mp[end];
for(int i = 0; i < 4; i ++)
{
int tx = x + dx[i] , ty = y + dy[i];
if(tx < 0 || tx >= 2 || ty < 0 || ty >= 3) continue;
string copy = update(old,tx,ty,x,y);
if(mp.count(copy)) continue;
mp[copy] = mp[old] + 1;
q.emplace(copy,tx,ty);
}
}
return -1;
}
};
6360. 等值距离和¶
相同元素分组+考虑增量 2023年4月9日
给你一个下标从 0 开始的整数数组 nums 。现有一个长度等于 nums.length 的数组 arr 。对于满足 nums[j] == nums[i] 且 j != i 的所有 j ,arr[i] 等于所有 |i - j| 之和。如果不存在这样的 j ,则令 arr[i] 等于 0 。
返回数组 arr 。
数据范围
1 <= nums.length <= 1050 <= nums[i] <= 109
输入输出
思路¶
相同元素分组+考虑增量
分组后,对于其中一个组 \(v\) ,先暴力计算出 \(v[0]\) 到其他元素的距离之和,设为 \(sum\)
然后考虑一般的,从\(v[i-1]\) 到 \(v[i]\) :
-
对于 \(0,1...,i-1\) 结点来说,到 \(v[i]\) 的距离相比于到 \(v[i-1]\) 的距离多了 \(v[i]-v[i-1]\)
-
对于 \(i,i-1...,v.size()-1\) 来说,到 \(v[i]\) 的距离相比于到 \(v[i-1]\) 的距离少了 \(v[i]-v[i-1]\)
体现到公式上来说,可以用递推的思想,将各元素的距离之和依次计算出来
代码
#include <bits/stdc++.h>
using namespace std;
#define DE(x) cerr << __LINE__ << " " << #x << " = " << x << " "
using ll = long long;
class Solution {
public:
vector<long long> distance(vector<int>& nums) {
int n = nums.size();
vector<long long > ans(n,0);
unordered_map<int,vector<int>> mp;
for(int i = 0; i < n; i ++) {
mp[nums[i]].push_back(i);
}
for(auto [x,v] : mp) {
ll sum = 0;
for(int i = 0; i < v.size(); i ++)
sum += v[i] - v[0];
ans[ v[0] ] = sum;
for(int i = 1; i < v.size(); i ++)
{
ll t = v[i] - v[i-1];
sum -= (v.size()-i) * t;
sum += i * t;
ans[ v[i] ] = sum;
}
}
return ans;
}
};
2602. 使数组元素全部相等的最少操作次数¶
排序 二分 2023年4月9日
给你一个正整数数组 nums 。
同时给你一个长度为 m 的整数数组 queries 。第 i 个查询中,你需要将 nums 中所有元素变成 queries[i] 。你可以执行以下操作 任意 次:
- 将数组里一个元素 增大 或者 减小
1。
请你返回一个长度为 m 的数组 answer ,其中 answer[i]是将 nums 中所有元素变成 queries[i] 的 最少 操作次数。
注意,每次查询后,数组变回最开始的值。
数据范围
n == nums.lengthm == queries.length1 <= n, m <= 1051 <= nums[i], queries[i] <= 109
输入输出
思路¶
利用前缀和,快速计算比 x 小的面积 和 比 x 大的面积
二分确定位置后加 \(1\) 是为了与前缀和的 1 base 统一
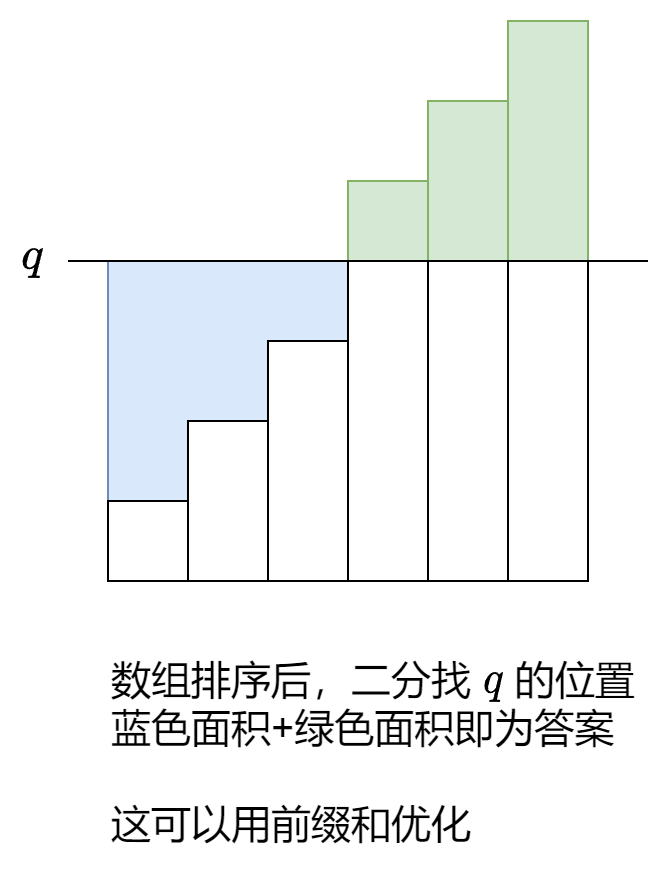
代码
#include <bits/stdc++.h>
using namespace std;
#define DE(x) cerr << __LINE__ << " " << #x << " = " << x << " "
using ll = long long ;
class Solution {
public:
vector<long long> minOperations(vector<int>& a, vector<int>& b) {
int n = a.size() , m = b.size();
sort(a.begin(), a.end());
vector<ll> s(n+1);
vector<ll> res;
for(int i = 1; i <= n; i ++) s[i] = s[i-1] + a[i-1];
// 利用前缀和,快速计算比 x 小的面积 和 比 x 大的面积
// 省去遍历一遍
// 1 base
// 闭区间
for(auto x : b) {
auto p = lower_bound(a.begin(), a.end(),x) - a.begin() + 1; // 这里加 1 是为了与前缀和的 base 统一
ll left = x * (p-1) - s[p - 1]; // 前 p - 1 个
ll right = s[n] - s[p - 1] - (n - p + 1) * x; // 从第 p 个到 第 n 个
res.emplace_back(left + right);
}
return res;
}
};
6359. 最小化数对的最大差值¶
二分答案 最大值最小化 2023年4月9日
给你一个下标从 0 开始的整数数组 nums 和一个整数 p 。请你从 nums 中找到 p 个下标对,每个下标对对应数值取差值,你需要使得这 p 个差值的 最大值 最小。同时,你需要确保每个下标在这 p 个下标对中最多出现一次。
对于一个下标对 i 和 j ,这一对的差值为 |nums[i] - nums[j]| ,其中 |x| 表示 x 的 绝对值 。
请你返回 p 个下标对对应数值 最大差值 的 最小值 。
数据范围
1 <= nums.length <= 1050 <= nums[i] <= 1090 <= p <= (nums.length)/2
输入输出
思路¶
因为要找最小值,最小值一定是在 nums 数组中相邻的位置产生
check 中为了解决不相邻的问题,如果选中当前元素,自动向跳两格
代码
#include <bits/stdc++.h>
using namespace std;
#define DE(x) cerr << __LINE__ << " " << #x << " = " << x << " "
using ll = long long ;
class Solution {
public:
int minimizeMax(vector<int>& nums, int p) {
sort(nums.begin(), nums.end());
int n = nums.size();
int m = n - 1;
vector<int> dif(m);
for(int i = 0; i < m; i ++)
dif[i] = nums[i+1] - nums[i];
auto check = [&](int x) {
int cnt = 0;
for(int i = 0; i < m; i ++)
if(dif[i] <= x) {
cnt ++;
i ++;
}
return cnt >= p;
};
int l = 0 , r = 1e9+2;
while(l<r)
{
int mid = l + r >> 1;
if(check(mid))
r = mid;
else
l = mid + 1;
}
return l;
}
};
1552. 两球之间的磁力¶
二分 最小值最大化 2023年4月9日
在代号为 C-137 的地球上,Rick 发现如果他将两个球放在他新发明的篮子里,它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子,第 i 个篮子的位置在 position[i] ,Morty 想把 m 个球放到这些篮子里,使得任意两球间 最小磁力 最大。
已知两个球如果分别位于 x 和 y ,那么它们之间的磁力为 |x - y| 。
给你一个整数数组 position 和一个整数 m ,请你返回最大化的最小磁力。
数据范围
n == position.length2 <= n <= 10^51 <= position[i] <= 10^9- 所有
position中的整数 互不相同 。 2 <= m <= position.length
输入输出
思路¶
check 中尽量让更多的篮子放入球
代码
#include <bits/stdc++.h>
using namespace std;
#define DE(x) cerr << __LINE__ << " " << #x << " = " << x << " "
using ll = long long ;
class Solution {
public:
int maxDistance(vector<int>& p, int m) {
int n = p.size();
sort(p.begin(), p.end());
auto check = [&](int x) {
int cnt = 1;
int j = 0;
for(int i = 1; i < n; i ++)
if(p[i] - p[j] >= x)
cnt ++ , j = i;
return cnt >= m;
};
int l = 0 , r = 1e9 + 2;
while(l < r)
{
int mid = l + r + 1>> 1;
if(check(mid))
l = mid;
else
r = mid - 1;
}
return l;
}
};
34. 在排序数组中查找元素的第一个和最后一个位置¶
二分 2023年4月9日
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
思路¶
lower_bound 返回大于 target 的第一个元素

代码
#include <bits/stdc++.h>
using namespace std;
#define DE(x) cerr << __LINE__ << " " << #x << " = " << x << " "
using ll = long long ;
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int start = lower_bound(nums.begin(), nums.end(),target) - nums.begin();
if(start == nums.size() || nums[start] != target) return {-1,-1};
int end = lower_bound(nums.begin(), nums.end(),target + 1) - nums.begin() - 1; //减一就是为了找到该元素的最后位置
return {start,end};
}
};
802. 找到最终的安全状态¶
toposort 2023年4月10日
拓扑排序¶
就是将图中的所有节点展开成一维序列,对于序列中任意的节点 \((u,v)\),如果在序列中 \(u\) 在 \(v\) 的前面,则说明在图中存在从 \(u\) 出发达到 \(v\) 的通路,即 \(u\) 排在 \(v\) 的前面。反之亦然。
在图论中,一个有向无环图必然存在至少一个拓扑序与之对应,反之亦然。
因此,对于有向图的拓扑排序,我们可以使用如下思路输出拓扑序(BFS 方式):
- 起始时,将所有入度为 \(0\) 的节点进行入队(入度为 \(0\),说明没有边指向这些节点,将它们放到拓扑排序的首部,不会违反拓扑序定义);
- 从队列中进行节点出队操作,出队序列就是对应我们输出的拓扑序。 对于当前弹出的节点 \(x\),遍历 \(x\) 的所有出度,即遍历所有由 \(x\) 直接指向的节点 \(y\),对 \(y\) 做入度减一操作(因为 \(x\) 节点已经从队列中弹出,被添加到拓扑序中,等价于从 \(x\) 节点从有向图中被移除,相应的由 \(x\) 发出的边也应当被删除,带来的影响是与 \(x\) 相连的节点 \(y\) 的入度减一);
- 对 \(y\) 进行入度减一之后,检查 \(y\) 的入度是否为 \(0\),如果为 \(0\) 则将 \(y\) 入队(当 \(y\) 的入度为 \(0\),说明有向图中在 \(y\) 前面的所有的节点均被添加到拓扑序中,此时 \(y\) 可以作为拓扑序的某个片段的首部被添加,而不是违反拓扑序的定义);
- 循环流程 \(2\)、\(3\) 直到队列为空。
如果一个图不是「有向无环图」的话,我们是无法将所有节点入队的,因此能够通过入队节点数量是否为 nnn 来判断是否为有向无环图。
思路¶
如果从该节点开始的所有可能路径都通向 终端节点 ,则该节点为 安全节点 。
正向拓扑排序的话,不一定所有路径都通向终端结点,但存在拓扑序
反向建图,拓扑完之后,把能通向终点的路径都删去了,还存在入度的一定不安全
代码
```c++
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
int n = graph.size();
vector<vector<int>> g(n);
vector<int> in(n);
for(int i = 0; i < n; i ++)
{
auto edge = graph[i];
for(auto x:edge)
g[x].emplace_back(i);
in[i] += edge.size();
}
// bfs 求反向图的拓扑排序
queue<int> q;
for(int i = 0; i < n; i ++)
if(in[i] == 0)
q.emplace(i);
while(q.size()) {
int x = q.front();
q.pop();
for(auto y:g[x]) {
in[y] -- ;
if(in[y] == 0)
q.push(y);
}
}
vector<int> ans;
for(int i = 0; i < n; i ++ )
if(in[i] == 0)
ans.emplace_back(i);
return ans;
}
};
```
851. 喧闹和富有¶
toposort 2023年4月10日
思路¶
需要从最穷的一直遍历到最富的
因为只遍历有 [直接边] 相连的会造成更新不完全,有些并没有遍历到,有些需要经过几个边才能到的
所以说从最穷的遍历到最富的,结果的贡献值依次传递,在计算中间的时候,前面已经计算过的就不需要再看啦
代码
#include <bits/stdc++.h>
using namespace std;
#define DE(x) cerr << __LINE__ << " " << #x << " = " << x << " "
#define eb emplace_back
#define pb push_back
using ll = long long ;
/* ************************************************ */
class Solution {
public:
vector<int> loudAndRich(vector<vector<int>>& richer, vector<int>& quiet) {
int n = quiet.size();
vector< vector<int> > g(n);
vector<int> in(n);
// 穷人指向富人,最穷的没有入度
for(auto rich:richer) {
int a = rich[0], b = rich[1];
g[a].eb(b);
in[b] ++;
}
// bfs 跑拓扑排序
queue<int> q;
for(int i = 0; i < n; i ++)
if(in[i] == 0)
q.push(i);
vector<int> ans(n);
while(q.size())
{
int x = q.front();
q.pop();
for(auto y:g[x]) {
in[y] -- ;
// 如果富人比穷人安静值小,则更新穷人的ans
if(quiet[ans[y]] < quiet[ans[x]]) ans[x] = ans[y];
if(in[y] == 0) q.push(y);
}
}
return ans;
}
};
920. 播放列表的数量¶
思路¶
只要听 \(l\) 首歌,在 \(n\) 首歌中选,
- 状态定义为
f[i][j],\(i\) 表示当前是第几首歌,\(j\)表示从前 \(j\) 首中选 - 每首歌至少播放一次,靠最后的 \(n\) 来保证
- 一首歌再次播放,\(j > k\) 时更新,可能选的数目为 \(j-k\) 个,指已经播放过的歌曲
Py代码
```python class Solution: def numMusicPlaylists(self, n: int, l: int, k: int) -> int: @cache def dp(i,j): # i 表示第几首歌,j表示从前 j 首中选
约 2434 个字 1702 行代码 预计阅读时间 29 分钟
if i == 0:
return 1 if j == 0 else 0
ans = dp(i-1, j-1) * (n-j+1) # 有 n - j + 1 中选法
ans += dp(i-1, j) * max(j-k, 0) # 如果 j > k 才能再次播放,能再次播放的是 j - k 个
return ans % (10**9 + 7)
return dp(l,n)
```
??? c++代码
```c++
class Solution {
public:
const int mod = 1e9+7;
int numMusicPlaylists(int n, int l, int k) {
long long f[110][110];
f[0][0] = 1;
for(int i = 1; i <= l; i ++)
for(int j = 1; j <= n; j ++)
{
f[i][j] = f[i-1][j-1] * (n-j+1);
if(j > k)
f[i][j] += f[i-1][j] * (j - k);
f[i][j] %= mod;
}
return f[l][n];
}
};
```
1041. 困于环中的机器人¶
模拟 2023年4月11日
他无论是走了 \(1/4,2/4,3/4,4/4\)圈,循环四遍肯定能到终点
代码
class Solution {
public:
int dx[4] = {0,1,0,-1};
int dy[4] = {1,0,-1,0};
// 上右下左
bool isRobotBounded(string instructions) {
int j = 0;
int a = 0, b = 0;
for(int i = 0; i < 4; i ++)
{
for(auto c:instructions) {
if( c == 'G') {
a = a + dx[j];
b = b + dy[j];
}
if( c == 'L')
j = (j - 1 + 4)%4;
if( c == 'R')
j = (j + 1 + 4)%4;
// cout << a << " " << b << "\n";
}
}
return a == 0 and b == 0;
}
};
863. 二叉树中所有距离为 K 的结点¶
bfs 2023年4月12日
思路¶
树是一类特殊的图,我们可以通过将二叉树转换为图的形式
对于二叉树中相互连通的节点(root 与 root.left、root 和 root.right),建立一条无向边。
然后跑一遍 BFS ,找到所有距离为 \(k\) 的点即可
代码
class Solution {
public:
vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {
vector<int> ans;
vector<vector<int>> g(510);
function<void(TreeNode*)> dfs = [&](TreeNode* cur) -> void {
if(cur == NULL) return ;
if(cur->left) {
g[cur->val].push_back(cur->left->val);
g[cur->left->val].push_back(cur->val);
dfs(cur->left);
}
if(cur->right) {
g[cur->val].push_back(cur->right->val);
g[cur->right->val].push_back(cur->val);
dfs(cur->right);
}
};
dfs(root);
// bfs
queue<int> q;
vector<int> dis(510,-1);
int val = target->val;
q.emplace(val);
dis[val] = 0;
if(dis[val] == k)
ans.emplace_back(val);
while(q.size()) {
int x = q.front();
q.pop();
for(auto y: g[x]) {
if(dis[y] == -1) {
dis[y] = dis[x] + 1;
if(dis[y] == k)
ans.emplace_back(y);
q.emplace(y);
}
}
}
return ans;
}
};
1020. 飞地的数量¶
dsu dfs 2023年4月13日
其实也可以不用并查集来维护,这里为了整理下并查集的板子,用并查集来维护集合
对本题来说更一般的做法是,将边缘的陆地跑一遍 DFS 就行
下面分别给出两种方法的代码
??? 并查集 + DFS 代码
```c++
#include <bits/stdc++.h>
using namespace std;
#define DE(x) cout << __LINE__ << " " << #x << " = " << x << "\n"
#define eb emplace_back
#define pb push_back
using ll = long long ;
/* ************************************************ */
class Solution {
public:
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
const int N = 400010;
int numEnclaves(vector<vector<int>>& g) {
int n = g.size() , m = g[0].size();
vector<int> p(n*m + 100);
// 并查集
p.clear();
function<int(int)> find = [&](int x) {
if(p[x] == x) return p[x];
return p[x] = find(p[x]);
};
auto query = [&](int a,int b) {
return find(a) == find(b);
};
auto unions = [&](int a,int b) {
p[find(a)] = find(b);
};
auto getIdx = [&](int x,int y) {
return x*m + y + 1;
};
// 并查集
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
p[getIdx(i,j)] = getIdx(i,j);
function<void(int ,int)> dfs = [&](int x,int y){
unions(getIdx(x,y), 0);
for(int i = 0; i < 4; i ++) {
int tx = x + dx[i], ty = y + dy[i];
if(tx < 0 || tx >= n || ty < 0 || ty >= m) continue;
if(g[tx][ty] == 1 && !query(getIdx(tx,ty),0)) {
dfs(tx,ty);
}
}
};
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (i == 0 || j == 0 || i == n - 1 || j == m - 1) {
if (g[i][j] != 1 || query(getIdx(i, j), 0)) continue;
dfs(i, j);
}
int ans = 0;
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
if(g[i][j] == 1 and !query(getIdx(i,j),0))
ans ++;
return ans;
}
};
```
普通dfs
class Solution {
public:
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
int numEnclaves(vector<vector<int>>& g) {
int n = g.size(), m = g[0].size();
int cnt = 0; // 网格中 1 的个数
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
if(g[i][j] == 1)
cnt ++;
vector<vector<bool>> st(n,vector<bool>(m,0));
function<void(int,int)> dfs = [&](int x,int y) -> void {
if(st[x][y] == 1) return;
st[x][y] = 1;
cnt--;
for(int i = 0; i < 4; i ++)
{
int tx = x + dx[i], ty = y + dy[i];
if(tx < 0 or tx >= n or ty < 0 or ty >=m) continue;
if(g[tx][ty] == 1 and st[tx][ty] == 0) {
dfs(tx,ty);
}
}
};
// 让边界的1跑dfs
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i == 0 || j == 0 || i == n - 1 || j == m - 1) {
if (g[i][j] != 1 || st[i][j]) continue;
dfs(i, j);
}
}
}
return cnt;
}
};
6353. 网格图中最少访问的格子数¶
bfs 平衡树 2023年4月13日
直接 BFS 在更新点时每次的复杂度都是 \(O(n)\) ,进而整个时间复杂度为 \(O(mn (m+n))\)
使用平衡树维护未访问过的位置,加速找到下个未访问位置。
实现时可以插入哨兵节点,避免二分查找迭代到非法位置。
- 时间复杂度: \(O(mn \log( \max(m,n)))\)
- 空间复杂度: \(O(mn)\)。
代码
#include <bits/stdc++.h>
using namespace std;
#define DE(x) cerr << __LINE__ << " " << #x << " = " << x << " "
#define eb emplace_back
#define pb push_back
using ll = long long ;
/* ************************************************ */
class Solution {
using Node = tuple<int,int,int>;
public:
int minimumVisitedCells(vector<vector<int>>& g) {
int n = g.size() , m = g[0].size();
queue<Node> q;
q.emplace(1,0,0);
vector<set<int>> rows_set(n),cols_set(m);
for (auto& row : rows_set) {
for (int j = 0; j <= m; ++j) {
row.insert(j);
}
}
for (auto& col : cols_set) {
for (int i = 0; i <= n; ++i) {
col.insert(i);
}
}
while(q.size()) {
auto [step,x,y] = q.front();
q.pop();
if(x == n-1 and y == m-1) {
return step;
}
auto & row = rows_set[x];
for(auto j = row.lower_bound(y+1); *j < min(g[x][y]+y+1,m); j = row.erase(j)) {
q.emplace(step+1,x,*j);
}
auto& col = cols_set[y];
for(auto i = col.lower_bound(x+1); *i < min(g[x][y]+x+1,n); i = col.erase(i)) {
q.emplace(step+1,*i,y);
}
}
return -1;
}
};
1054. 距离相等的条形码¶
贪心 2023年4月14日
按照频率排序,用优先队列来维护
res 存储序列,每次模拟即可
一定是频率最大的先放,然后频率次大的,在频率最大的,在频率次大的,这样依次迭代,因为题目保证有解,这样划分一定可以得到最后的序列
代码
class Solution {
public:
vector<int> rearrangeBarcodes(vector<int>& b) {
priority_queue<pair<int, int>> q;
unordered_map<int,int> mp;
for(auto x: b){
mp[x]++;
}
for(const auto &[k, v]: mp) {
q.push({v, k});
}
vector<int> res;
while(q.size()) {
auto [v, k] = q.top(); q.pop();
if(res.empty() || res.back() != k) {
res.push_back(k);
if(--v) q.push({v, k});
}else{
if(q.size() < 1) return res;
auto [y, x] = q.top(); q.pop();
res.push_back(x);
if(--y) q.push({y, x});
q.push({v, k});
}
}
return res;
}
};
2080. 区间内查询数字的频率¶
二分 2023年4月15日
思路¶
要求的是一个数,在一个区间内出现的次数
我们先把每个数出现的下标存下来,再用二分看看区间中有多少个下标,即为次数
代码
#include <bits/stdc++.h>
using namespace std;
#define DE(x) cout << __LINE__ << " " << #x << " = " << x << "\n"
#define eb emplace_back
#define pb push_back
using ll = long long ;
/* ************************************************ */
class RangeFreqQuery {
public:
map<int,vector<int>> mp;
RangeFreqQuery(vector<int>& arr) {
int n = arr.size();
for(int i = 0; i < n; i ++)
mp[arr[i]].eb(i);
}
int query(int left, int right, int value) {
auto l = lower_bound(mp[value].begin(), mp[value].end(),left);
auto r = upper_bound(mp[value].begin(), mp[value].end(),right);
return r - l;
}
};
dfs 应用题¶
题目分析
对每种基料来说,\(m\) 种配料每次都有三种选择
直接 DFS 即可
时间复杂度:\(O(n* 3^m)\)
代码
class Solution {
public:
int closestCost(vector<int>& a, vector<int>& b, int target) {
int n = a.size();
int m = b.size();
int ans = -1;
function<void(int,int)> dfs = [&](int op,int sum) {
if(op == m) {
if(ans == -1 or abs(sum - target) < abs(target - ans) or (abs(sum - target) == abs(target - ans) and sum < ans))
ans = sum;
return ;
}
dfs(op + 1,sum);
dfs(op + 1,sum + b[op]);
dfs(op + 1,sum + 2*b[op]);
};
for(int i = 0; i < n; i ++)
dfs(0,a[i]);
return ans;
}
};
958. 二叉树的完全性检验¶
树的层序遍历 2023年4月15日
层序遍历序列中,完全二叉树不能存在 NULL , 1 这种情况,在空值之后只能全为空值,否则不为完全二叉树、
代码
class Solution {
public:
bool isCompleteTree(TreeNode* root) {
if(root == NULL) return false;
queue<TreeNode*> q;
q.emplace(root);
bool findNULL = false;
while(q.size()) {
int n = q.size();
for(int i = 0; i < n; i ++) {
auto t = q.front();
q.pop();
if(t == NULL and findNULL == 0) findNULL = 1;
else if(t and findNULL) return false;
else if(t and !findNULL){
q.emplace(t->left);
q.emplace(t->right);
}
}
}
return true;
}
};
求下一个更大的数¶
单调栈 2023年4月16日
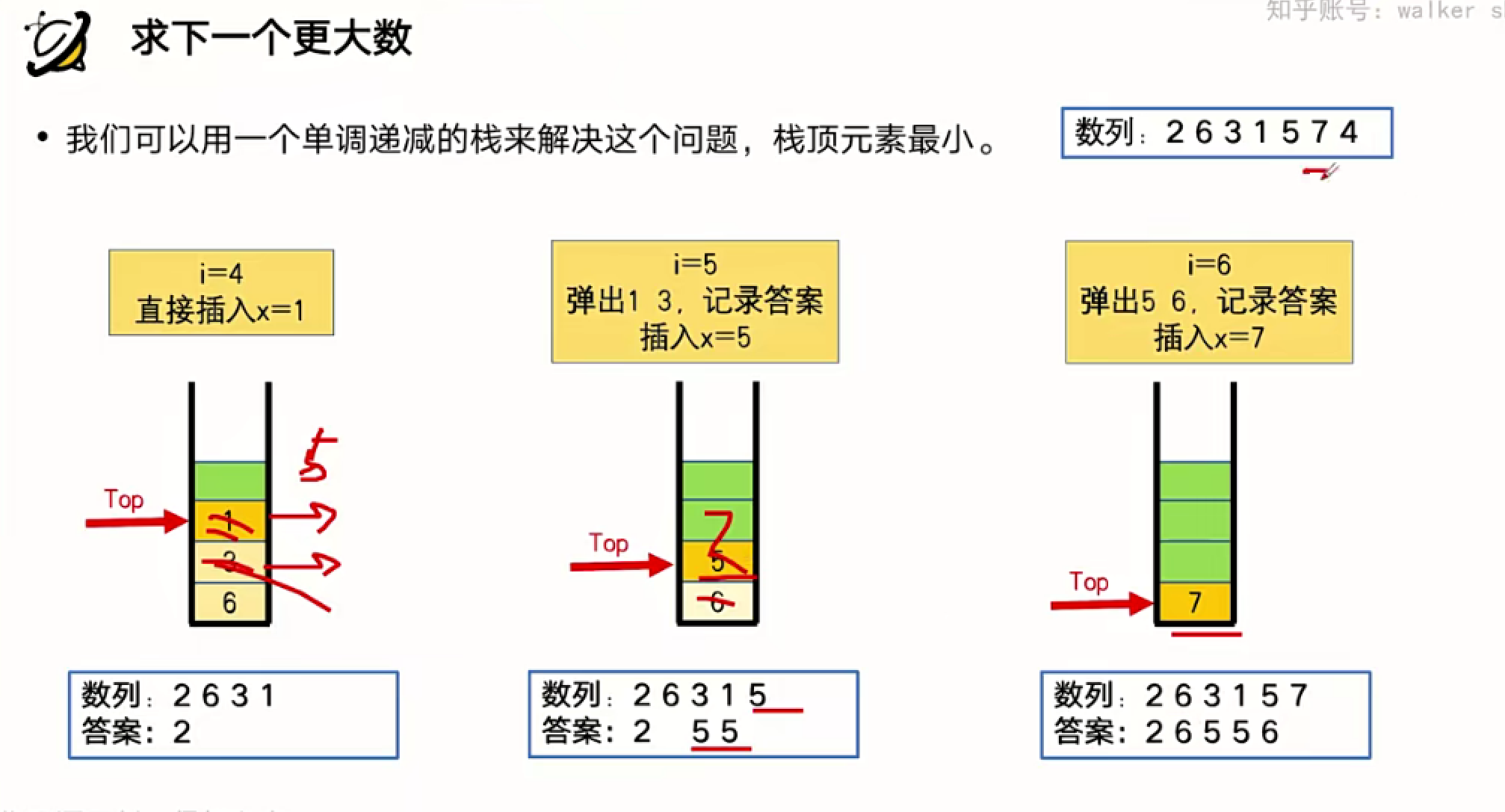
单调栈(monotonic stack)是栈的一种特殊应用,它主要用于解决一类关于数组的单调性问题。
- 维护栈的单调性
- 在出栈时记录答案
单调栈的时间复杂度为 \(O(n)\),空间复杂度为 \(O(n)\)。
题目分析
栈中维护的是单调递减的序列 求下一个更大的值 (严格,不包含相等)
这里,我将左边更大的和右边更大的分别求出来了,供读者参考
代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define eb emplace_back
#define pb push_back
#define DE(x) cerr << __LINE__ << " " << #x << " = " << x << "\n"
int n,m;
const int mod = 998244353;
const int N = 1e6;
void solve()
{
cin >> n;
vector<int> a(n);
for(int i = 0; i < n; i ++)
cin >> a[i];
vector<int> right(n,n);
vector<int> left(n,-1);
stack<int> st;
// 栈中维护的是单调递减的序列
// 求下一个更大的值(严格,不包含相等)
for(int i = 0; i < n; i ++) {
while(st.size() and a[st.top()] >= a[i]) {
st.pop();
}
if(st.size()) {
left[i] = st.top();
}
st.push(i);
}
st = stack<int>();
for(int i = n-1;i >= 0 ; i --) {
while(st.size() and a[st.top()] >= a[i])
st.pop();
if(st.size())
right[i] = st.top();
st.push(i);
}
// for(int i = 0; i < n; i ++)
// cout << left[i] << " \n"[i==n-1];
// for(int i = 0; i < n; i ++)
// cout << right[i] << " \n"[i==n-1];
for(int i = 0; i < n; i ++)
cout << (right[i] == n ? 0 : (right[i] + 1)) << " \n"[i==n-1];
// for(int i = 0; i < n; i ++)
// cout << (left[i] == -1 ? 0: (left[i] + 1)) << " ";
}
int main()
{
std::ios::sync_with_stdio(0),std::cin.tie(0),std::cout.tie(0);
ll T = 1;
// cin >> T;
while (T--)
solve();
}
有一种简单的写法,适用于数组数组中各个元素不相同的,即不存在相等的值,可以扫一遍就能将左边和右边求出来
代码
vector<int> right(n,n);
vector<int> left(n,-1);
stack<int> st;
// 举例:2 6 3 1 5 7 4
// 0(2) 进栈
// right[0] = 1, 0(2) 出栈, 1(6) 进栈
// left[2] = 1, 2(3) 进栈
// 栈中维护的是单调递减的序列
// 求下一个更大的值
for(int i = 0; i < n; i ++) {
while(st.size() and a[st.top()] >= a[i]) {
right[st.top()] = i;
st.pop();
}
if(st.size()) {
left[i] = st.top();
}
st.push(i);
}
单调栈应用题¶
单调栈 2023年4月16日
面积 = 当前值作为区间最小值所在的最大区间的长度 * 当前值
用单调栈来维护下一个更小的值 严格小于
枚举所有点,找到最大的面积
代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define eb emplace_back
#define pb push_back
#define DE(x) cerr << __LINE__ << " " << #x << " = " << x << "\n"
int n,m;
const int mod = 998244353;
const int N = 1e6;
void solve()
{
cin >> n;
vector<int> a(n);
for(int i = 0; i < n; i ++)
cin >> a[i];
vector<int> right(n,n);
vector<int> left(n,-1);
stack<int> st;
for(int i = 0; i < n; i ++) {
while(st.size() and a[st.top()] >= a[i]) {
st.pop();
}
if(st.size()) {
left[i] = st.top();
}
st.push(i);
}
st = stack<int>();
for(int i = n-1;i >= 0 ; i --) {
while(st.size() and a[st.top()] >= a[i])
st.pop();
if(st.size())
right[i] = st.top();
st.push(i);
}
ll ans = 0;
for(int i = 0; i < n; i ++) {
int l = left[i] + 1, r = right[i] - 1; // 左闭右闭型
// cout << l << " " << r << " " << a[i] << "\n";
ll t = 1LL * (r-l+1)*a[i];
// DE(t);
ans = max(ans,t);
}
cout << ans << "\n";
}
int main()
{
std::ios::sync_with_stdio(0),std::cin.tie(0),std::cout.tie(0);
ll T = 1;
// cin >> T;
while (T--)
solve();
}
2281. 巫师的总力量和¶
二次前缀和 单调栈 2023年4月16日
如何计算子数组的元素和的和?
不妨将子数组的右端点固定,子数组左端点的范围是多少?
对于多个不同的右端点,其对应的左端点的范围是否均相同?

用单调栈来维护下一个更小的值
枚举所有点,找到最大的总力量
代码
#include <bits/stdc++.h>
using namespace std;
#define DE(x) cout << __LINE__ << " " << #x << " = " << x << " "
#define eb emplace_back
#define pb push_back
using ll = long long ;
/* ************************************************ */
class Solution {
public:
int totalStrength(vector<int>& a) {
int n = a.size();
vector<int> left(n,-1);
vector<int> right(n,n);
stack<int> st;
for (int i = 0; i < n; ++i) {
while (!st.empty() && a[st.top()] >= a[i]) {
right[st.top()] = i;
st.pop();
}
if (!st.empty()) left[i] = st.top();
st.push(i);
}
vector<ll> pre_1(n+3,0),pre_2(n+3,0);
ll ans = 0, mod = 1e9+7;
for(int i = 1; i <= n; i ++)
pre_1[i] = pre_1[i-1] + a[i-1];
for(int i = 1; i <= n; i ++)
pre_2[i+1] = (pre_2[i] + pre_1[i])%mod;
auto calu = [&](ll x,ll y) {
return (x%mod * y%mod)%mod;
};
for(int i = 0; i < n; i ++) {
long l = left[i] + 1, r = right[i] - 1; // [l,r] 左闭右闭
long tot = ((i - l + 1) * (pre_2[r + 2] - pre_2[i + 1]) - (r - i + 1) * (pre_2[i + 1] - pre_2[l])) % mod;
ans = (ans + a[i] * tot) % mod; // 累加贡献
}
return (ans + mod )%mod;
}
};
2645. 构造有效字符串的最少插入数¶
模拟 2023年4月16日
方法一
```c++
class Solution {
public:
int addMinimum(string s) {
int n = s.size();
// 最终序列是 012 012 012 这样循环
int cnt = 0;
int i = 0;
// cnt 要统计当前的数量,不能提前取模,用到的时候取个模就行。
// 不要想着一步到位,急急急
while(i < n) {
if(s[i] == ('a' + (cnt%3))) {
i ++;
}
cnt ++;
}
int r = cnt%3 ;
if(r!=0) cnt += 3 - r;
return cnt - n;
}
};
```
方法二
\(bac \(,\)b\) 在前一个 \(abc\),\(ac\) 在第二个 \(abc\)
就是存在 \(s[i] <= s[i-1]\) 这两个字母一定不在同一个 \(abc\) 中,看相邻的字母有递减的就 \(cnt++\)
\(cnt\) 表示最终 \(abc\) 的个数
结果就是 \(cnt*3 - n\)
代码
6335. 二叉树的堂兄弟节点 II¶
bfs 算两次 2023年4月16日
用 BFS 遍历二叉树,对于每一层:
-
首先,遍历当前层的每个节点,通过节点的左右儿子,计算下一层的节点值之和
nextLevelSum; -
然后,再次遍历当前层的每个节点
x,计算x的左右儿子的节点值之和childrenSum,更新xxx 的左右儿子的节点值为nextLevelSum − childrenSum
代码
class Solution {
public:
TreeNode* replaceValueInTree(TreeNode* root) {
vector<TreeNode*> q = {root};
root->val = 0;
while(q.size()) {
vector<TreeNode *> nxt;
int next_level_sum = 0; // 下一层的节点值之和
for (auto node: q) {
if (node->left) {
nxt.push_back(node->left);
next_level_sum += node->left->val;
}
if (node->right) {
nxt.push_back(node->right);
next_level_sum += node->right->val;
}
}
// 再次遍历,更新下一层的节点值
for (auto node: q) {
int child_sum = (node->left ? node->left->val : 0) +
(node->right ? node->right->val : 0);
if (node->left) node->left->val = next_level_sum - child_sum;
if (node->right) node->right->val = next_level_sum - child_sum;
}
q = move(nxt);
}
return root;
}
};
847. 访问所有节点的最短路径¶
bfs 2023年4月17日
存在一个由 n 个节点组成的无向连通图,图中的节点按从 0 到 n - 1 编号。
给你一个数组 graph 表示这个图。其中,graph[i] 是一个列表,由所有与节点 i 直接相连的节点组成。
返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止,也可以多次重访节点,并且可以重用边。
思路¶
这是一个等权无向图,题目要我们求从「一个点都没访问过」到「所有点都被访问」的最短路径。
所以我们将状态定义为:当前有那个顶点已经访问,求出到当前状态的最短路
在一般的 bfs 中 queue<int> q 中存储的是结点 u,st[N] 表示结点 u 是否访问过
而这里,当前状态是由 当前结点 u 和 当前已经被访问过的结点 mask 共同决定的,其中 mask 要用状态压缩来表示。
所以状态被定义为 {u,mask} ,\(st\) 数组用 \(dis\) 数组来代替,dis == INF 表示未被访问。
代码
const int N = 13,INF = 0x3f3f3f3f;
class Solution {
public:
bool st[N][1 << N];
int dis[N][1 << N];
int shortestPathLength(vector<vector<int>>& g) {
int n = g.size();
memset(dis,0x3f,sizeof dis);
// (u,mask)
queue<pair<int,int>> q;
// 多起点,把所有可能的起点丢点队列中
for(int i = 0; i < n; i ++) {
q.push({i,1 << i});
dis[i][1 << i] = 0;
}
while(q.size()) {
auto [u,mask] = q.front();
q.pop();
if(mask == (1 << n) - 1) {
return dis[u][mask];
}
for(auto v: g[u]) {
int state = mask | (1 << v);
if(dis[v][state] == INF) {
dis[v][state] = dis[u][mask] + 1;
q.push({v,state});
}
}
}
return -1;
}
};
909. 蛇梯棋¶
bfs 2023年4月18日
思路¶
最多有 \(20 \times 20\) 个格子,直接使用常规的单向 BFS 进行求解即可。
为了方便我们可以按照题目给定的意思,将二维的矩阵「扁平化」为一维的矩阵,然后再按照规则进行 BFS。
感觉这种题,更像是状态机一样,从一个状态 u 走向另一个状态 v,只不过走向状态 v 的道路不仅仅只有通过 v 这一条路,还有很多路,所以就是找到所有可能的路线,找最小值。(这不就是 dp ????)
时间复杂度:\(O(n^2)\),保证只会入队一次捏。
代码
const int N = 22,INF = 0x3f3f3f3f;
class Solution {
public:
int st[N*N];
int snakesAndLadders(vector<vector<int>>& g) {
int n = g.size(), m = g[0].size();
// bfs 模拟过程
memset(st,0,sizeof st);
// {u,dis}
queue<pair<int,int>> q;
q.push({1,0});
st[1] = true;
while(q.size()) {
auto [u,dis] = q.front();
q.pop();
if(u == n*n) {
return dis;
}
for(int i = u + 1; i <= min(u + 6,n*n); i ++) {
int v = i;
int x = n - 1 - (i - 1) / m;
int y = (i - 1) % m;
if((n - x)%2 == 0) y = m - 1 - y;
// 蛇或梯子
if(g[x][y] != -1) {
v = g[x][y];
}
if(st[v] == false) {
q.push({v,dis + 1});
st[v] = true;
}
}
}
return -1;
}
};
954. 二倍数对数组¶
模拟 2023年4月19日
思路¶
如果我们每次都拿最接近 \(0\) 的值作为起点,整个构造过程就是唯一确定的。
具体的,我们可以借助优先队列(堆)来实现,构造一个以与 \(0\) 值距离作为基准的小根堆。
逐一构造,每次构造最近接零的
设一对元素为 {a,b} , 其中 b = 2 * a
cnt 中存储 b 元素需要的次数
代码
class Solution {
public:
bool canReorderDoubled(vector<int>& a) {
int n = a.size();
std::priority_queue<int, std::vector<int>, std::function<bool(int, int)>> q(
[](int a, int b) {
return std::abs(a) > std::abs(b);
}
);
map<int,int> cnt;
for(int i = 0; i < n; i ++) {
q.push(a[i]);
}
// 逐一构造,每次构造最近接零的
// cnt中只存储 一对中的后面那个
// cnt[x,y] 表示 x 需要多少次才能一一构造。
while(q.size()) {
int x = q.top(),t = x*2;
q.pop();
if(cnt[2*x] != 0 and --cnt[2*x] >= 0) continue;
cnt[t*2] ++;
}
for(auto [x,y]: cnt) {
if(y != 0) return false;
}
return true;
}
};
Created: January 3, 2024