科学上分之旅¶
约 769 个字 39 行代码 预计阅读时间 3 分钟
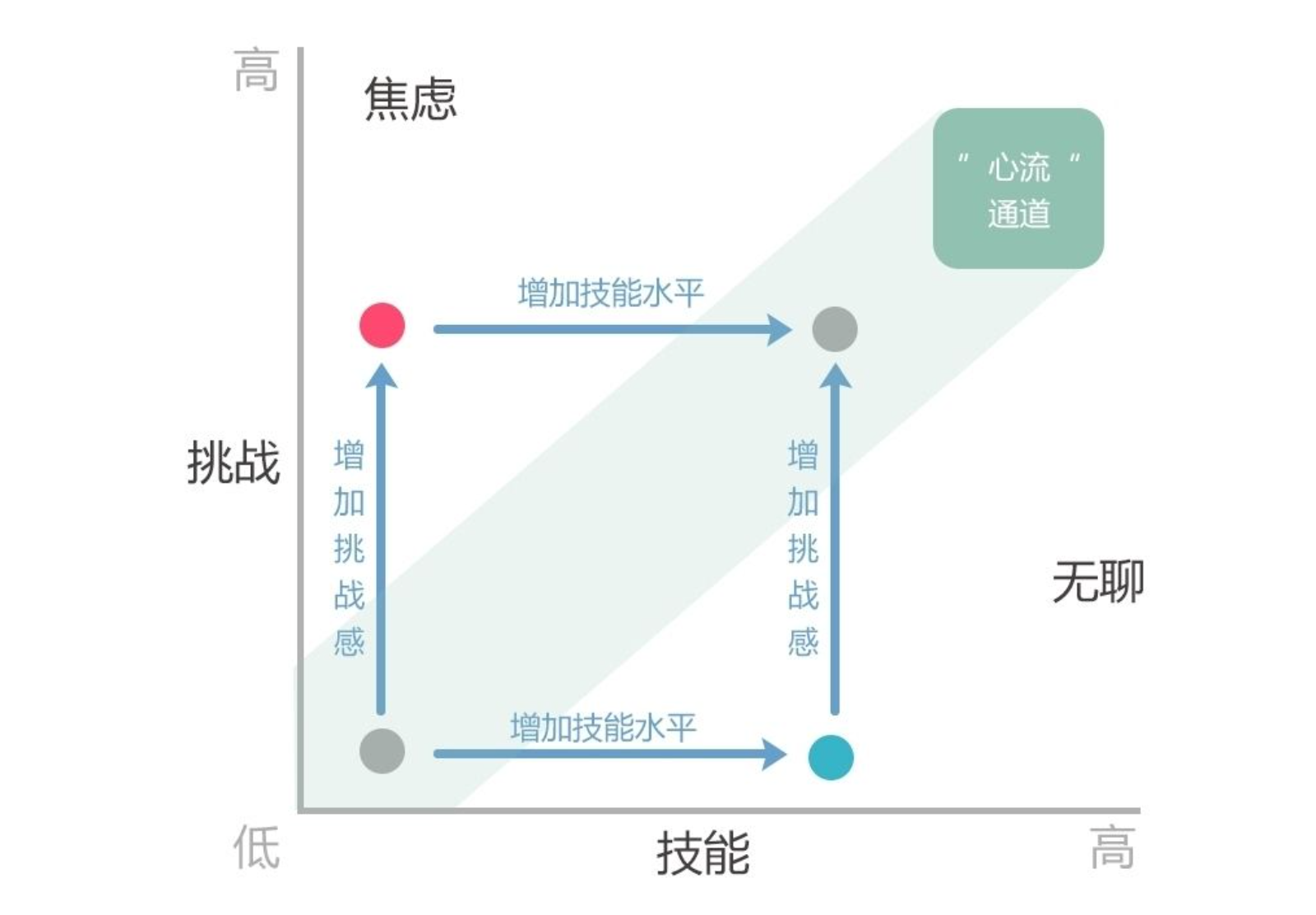
- 打开 https://zerotrac.github.io/leetcode_problem_rating/ ,表中的最后一列表示题目的难度,越高题目越难。
- 往后翻,做难度分与自己竞赛分接近的题目。
- 会做/不会做,就找难度分更高/更低的题目(比如会做难度分就 +25,不会做难度分就 −25)。
- 不断练习难度和自己实力相匹配的题目,保证自己处在一个合适的「心流通道」中。
5.30¶
区间相交¶
题目
You are given \(N\) intervals of real numbers. The \(i\)-th \((1 \leq i \leq N)\) interval is \([l_i, r_i]\). Find the number of pairs \((i, j)\,(1 \leq i < j \leq N)\) such that the \(i\)-th and \(j\)-th intervals intersect.
求区间相交的个数。
思路
对于区间 [l,r] ,有多少个区间在他之前 \(( l' \le l)\) 并且与他相交
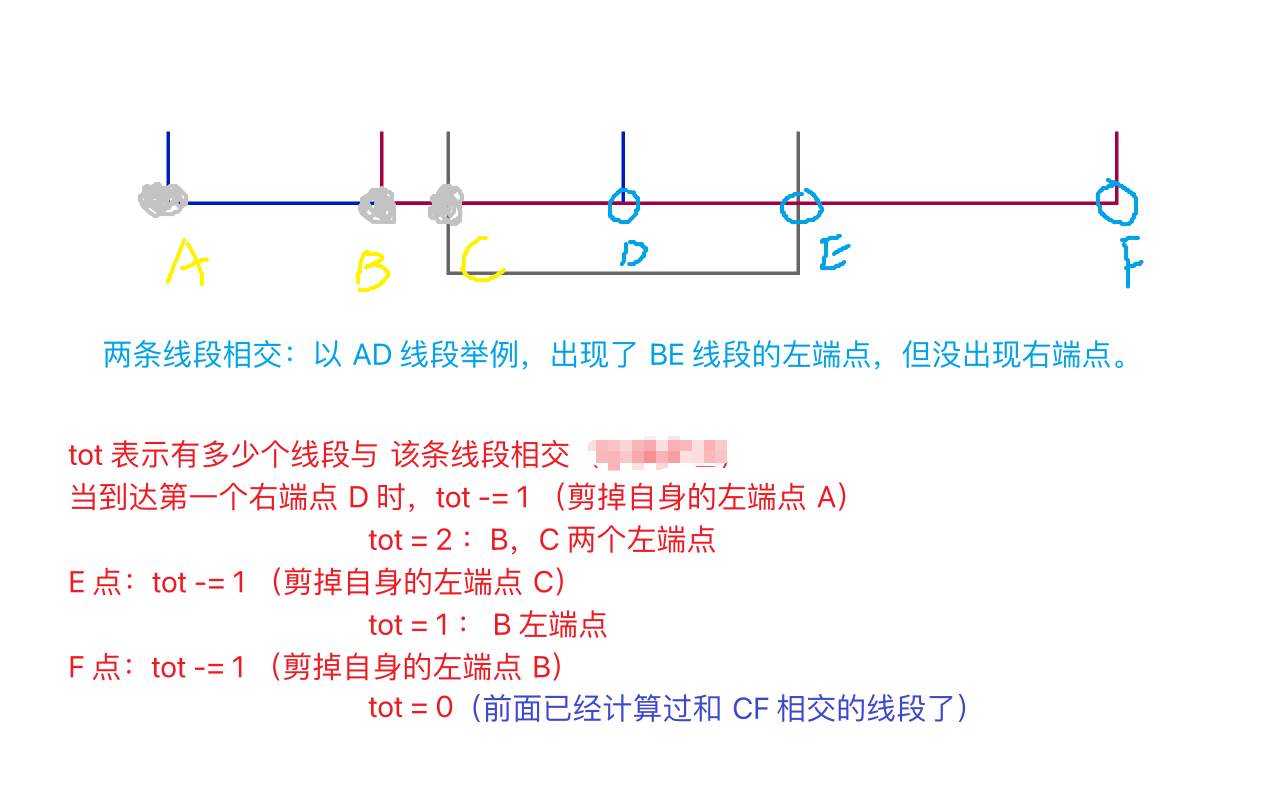
代码链接:AtCoder Beginner Contest 355d
另一种思路:
考虑有多少个区间不相交
问题转化为:对于每个 \(l\) ,有多少个 \(r'\) 满足
r' < l
对 \(l\) 和 r 分别排序,依次扫描每个 \(l\) ,同时看看有多少个 r 满足
r < l。核心代码如下
c++ long long res = n*(n-1)/2; j = 0; for(int i = 0; i < n; i ++) { while(j < n && r[j] < l[i]) j += 1; res -= j; }
5.31¶
滑动窗口¶
题目
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
思路
滑动窗口:用哈希表来维护从 l 到 r 的字符。
int lengthOfLongestSubstring(string s) {
int n = s.size(), l = 0, res = 0;
set<char> st;
for(int r = 0; r < n; r ++) {
while(st.count(s[r])) {
st.erase(s[l ++]);
}
st.insert(s[r]);
res = max(res,r - l + 1);
}
return res;
}
MST¶
题目
You are given a weighted undirected connected graph \(G\) with \(N\) vertices and \(N-1\) edges, where vertices are numbered \(1\) to \(N\) and edges are numbered \(1\) to \(N-1\). Edge \(i\) connects vertices \(a_i\) and \(b_i\) with a weight of \(c_i\). You are given \(Q\) queries to process sequentially. The \(i\)-th query is described as follows:
- You are given integers \(u_i, v_i, w_i\). Add an edge with weight \(w_i\) between vertices \(u_i\) and \(v_i\) in \(G\). Then, print the sum of the weights of the edges in a minimum spanning tree of \(G\).
对MST q 次加边,求MST的代价。
边权的范围:\(1 \leq c_i, w_i \leq 10\)
思路
实时维护最小生成树中有多少条 1-边 ,2-边 …… 10-边( “X-边“ 代表边权为 X 的边)
- 使用一个「批量版」的 Kruskal 算法
- 分别维护加入了所有 1-边,2-边 …… 10-边后的并查集
- 所以代价为:
1*1-边数量 + 2*2-边数量 + …… + 10*10-边数量
怎么知道 MST 中有多少条 X-边呢?
- 加入 X-边 之前的并查集中连通块的数量 \(-\) 加入 X-边 之后连通块的数量
代码链接:AtCoder Beginner Contest 355f
6.3¶
状态压缩¶
Submission #54211161 - AtCoder Beginner Contest 356
6.9¶
模拟¶
给你两个 正整数 n 和 k。有 n 个编号从 0 到 n - 1 的孩子按顺序从左到右站成一队。
最初,编号为 0 的孩子拿着一个球,并且向右传球。每过一秒,拿着球的孩子就会将球传给他旁边的孩子。一旦球到达队列的 任一端 ,即编号为 0 的孩子或编号为 n - 1 的孩子处,传球方向就会 反转 。
返回 k 秒后接到球的孩子的编号。
思路
首先判断k秒后传递的方向,n个数传递n-1秒到达最后一个位置,所有当k/(n-1)是奇数时表示当前传递方向反向,为偶数表示正向;再进行取余运算即可计算出当前所在的位置。
代码
暴力模拟
class Solution {
public:
int numberOfChild(int n, int k) {
int res = 0, d = 1;
for(int i = 0; i < k; i ++) {
res += d;
if(res == n - 1 or res == 0) d = - d;
}
return res;
}
};
数学算法 \(O(1)\)
class Solution {
public:
int numberOfChild(int n, int k) {
n --;
int r = k / n;
if(r & 1) return n - k % n;
return k % n;
}
};
Created: June 3, 2024