Skip to content

代码源初级DP

约 1917 个字 191 行代码 预计阅读时间 9 分钟

两个要求：

  • 最优子结构：大问题的解可以由小问题的解推出。问题拆解过程中不能无限递归！
  • 无后效性：未来与过去无关，一旦得到了一个小问题的解，如何得到它的解的过程不影响大问题的求解。

两个元素：

  • 状态：求解过程进行到了哪一步，可以理解为一个子问题。
  • 转移：从「小问题的解」推导到「大问题的解」的过程

动态规划概述

最短路

给定一幅 \(n(1 \le n \le 1000)\) 个点 \(m(1 \le m \le 1000)\)条边的有向图，每条边有个边权，代表经过这条边需要花费的时间，我们只能从编号小的点走到编号大的点，问从 \(1\) 号点走到 \(n\) 号点最少需要花费多少时间？

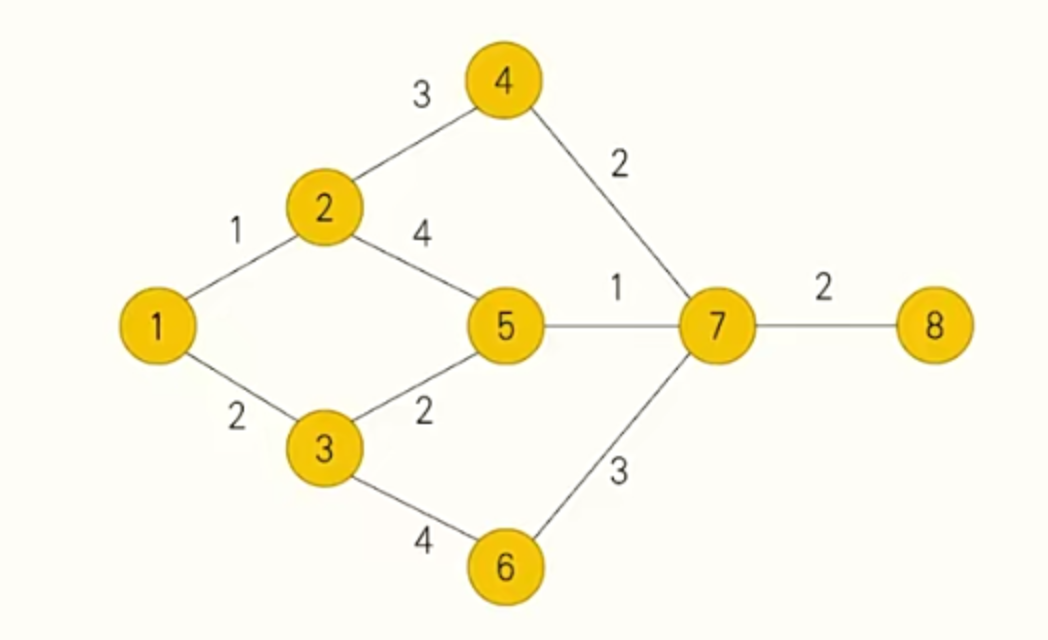
alt text

最优子结构：为了算出从 1 号点到 y 号店最少需要花费多少时间，我们可以先计算出所有和 y 号店右边相连，并且标号小于 y 号点的 x，从 1 号点到 x 号店最少需要花费多少时间，然后再推导 y 号点的情况。

无后效性：我们只关系到每个点最少花费多少时间，不关心具体走了哪条路径。

状态：用 f[i] 表示从 1 号点到 i 号店最少需要花费多少时间

转移：f[y] = min(f[y],f[x] + e[x][y])

最长上升子序列

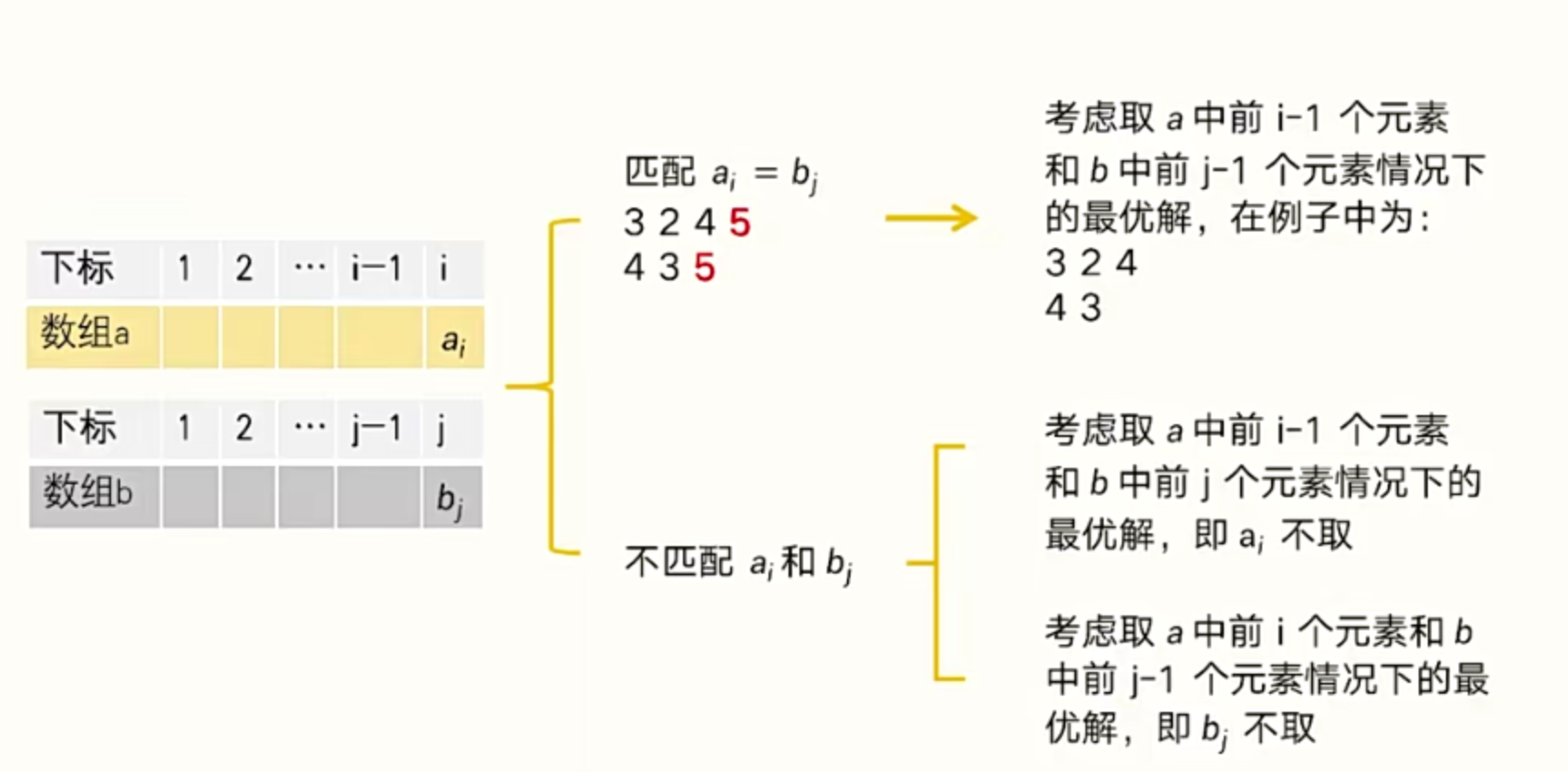
alt text

最长公共子序列

两个数组，所以二维

alt text

alt text

最长回文子串

给定一个长度为 \(n\) 的数组 \(a_1, a_2, \ldots, a_n\)，问其中的最长回文子串长度。

定义子串 \(a_l, a_{l+1}, \ldots, a_r\) 为回文子串，当且仅当这个子串正着看和反着看是一样的，即有 \(a_l=a_r, a_{l+1}=a_{r-1}, \ldots\)。

思想

回文串两边加上两个相同字符，会形成一个新的回文串 。

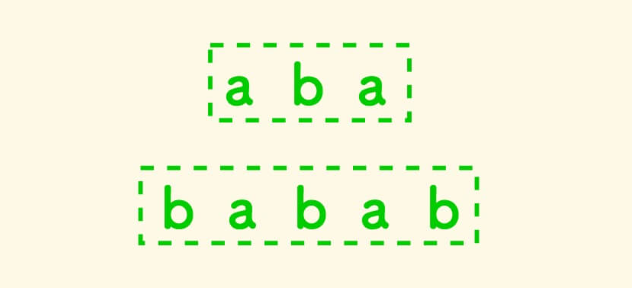
alt text

\(dp[i][j]\) 记录从 i 到 j 是否为回文串。

如果 \(s[i] == s[j]\) 且 \(dp[i+1][j-1] = \text{True}\) 时，\(dp[i][j] = \text{True}\)。

核心代码

memset(f,0,sizeof(f));
for(int i = 1; i <= n; i ++) f[i][i] = 1;

int res = 1;
// f[i][j] = f[i+1][j-1]: i 倒序，j 正序
for(int i = n; i >= 1; i --) {
    for(int j = i; j <= n; j ++) {
        if(a[i] == a[j]) { // 向下递归
            if(j - 1 >= i + 1) { 
                // aAa 这种情况
                f[i][j] = f[i+1][j-1];
            } else {
                // aa 这种情况
                f[i][j] = 1;
            }
        }
        if(f[i][j] == 1) {
            res = max(res,j - i + 1);
        }
    }
}
cout << res;

背包问题

概述

  • 01背包：每件物品只能选一次

  • 完全背包：每件物品能选无限次

  • 多重背包：每件物品选的次数是有限制的

  • 二维费用的背包
  • 分组背包：每组里面只能选一个

从实际含义出发，推递推公式。

  • 从上一层推：从大到小枚举（防止小的先更新）
  • 从本层推，从小到大枚举。

体积从大到小枚举只能选一个（01背包），体积从小到大枚举可以选多个（完全背包）

01背包

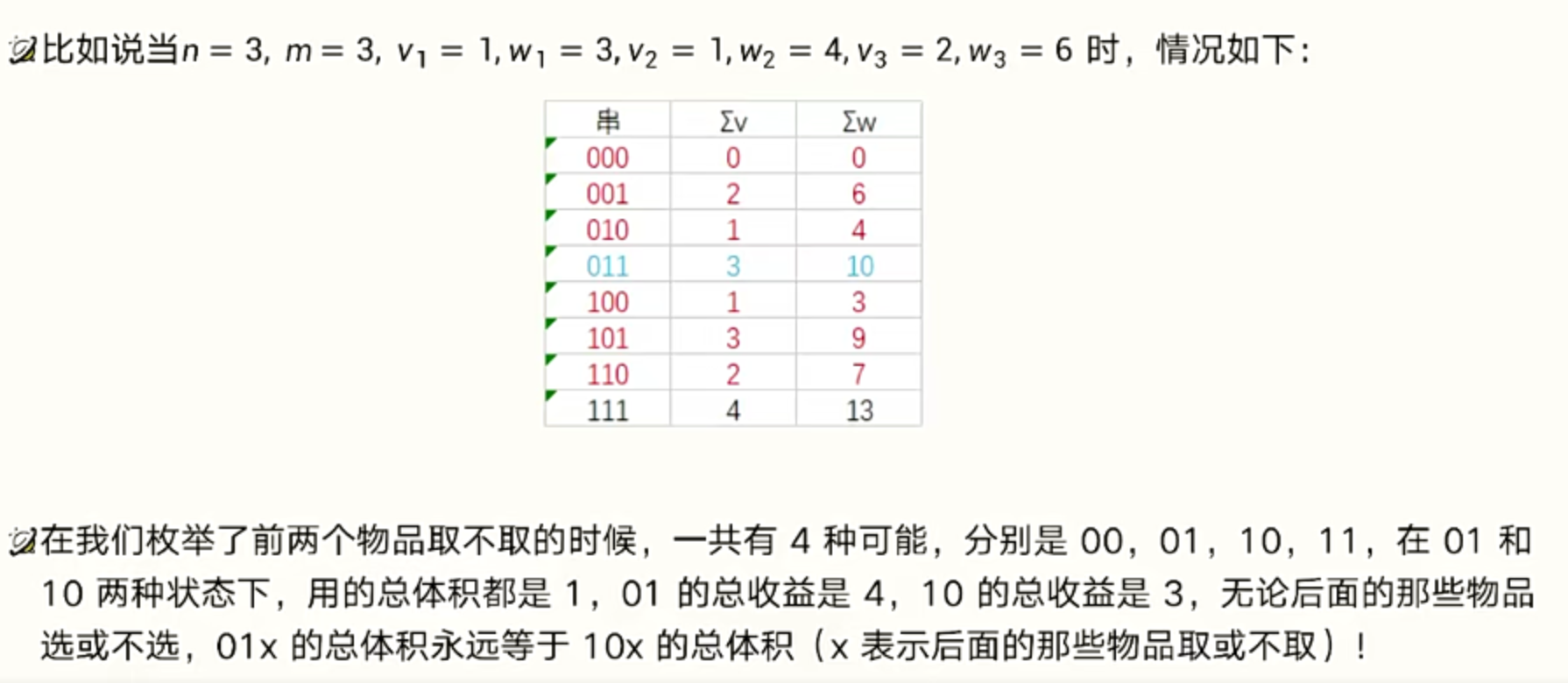
image-20240219140050931

当我们考虑了前 i 个物品取或不取，如果有两组方案的总体积是一样的，那么我们只需要保留总收益最大的那组

考虑前 \(i\) 个物品，总体积为 \(j\) 时分为两种情况

  • 第 \(i\) 个物品没取：问题变成了考虑前 \(i - 1\) 个物品，总体积为 \(j\) 时的情况
  • 第 \(i\) 个物品取了：问题变成了考虑前 \(i - 1\) 个物品，总体积为 \(j - v_i\) 的情况

从后到前枚举体积：f[j] = f[j - v[i]] + w[i] ,其中 f[j - v[i]] 是上一层的情况

f[i][j] 可以从 f[i-1][0],f[i-1][1] .... f[i-1][j - v[i]] 中转移过来

for(int i = 1; i <= n; i ++)
    for(int j = m; j >= v[i]; j --)
        f[j] = max(f[j],f[j - v[i]] + w[i]);

完全背包

考虑前 \(i\) 个物品，总体积为 \(j\) 时分为两种情况

  • 第 \(i\) 个物品没取：问题变成了考虑前 \(i - 1\) 个物品，总体积为 \(j\) 时的情况
  • 第 \(i\) 个物品取了：问题变成了考虑前 \(i\) 个物品，总体积为 \(j - v_i\) 的情况

从前到后枚举体积：f[j] = f[j-v[i]] + w[i]，其中 f[j - v[i]] 是本层的情况。

for(int i = 1; i <= n; i ++)
    for(int j = v[i]; j <= m; j ++)
        f[j] = max(f[j],f[j - v[i]] + w[i]);

多重背包

第 i 中物品可以使用 \(l_i\) 次，我们可以把它拆成 \(l_i\) 个物品，每个物品只能使用一次。

这样就转化为 01背包问题啦！

核心代码

复杂度：\(O(n^3)\)

for(int i = 1; i <= n; i ++)
    for(int k = 1; k <= l[i]; k ++)
    for(int j = m; j >= v[i]; j --)
        f[j] = max(f[j],f[j-v[i]] + w[i]);

二进制优化，时间复杂度：\(n v\log l\) 

for(int i = 1; i <= n; i ++) {
    int res = l[i];
    // 1 2 4 8 的 01背包
    for(int k = 1; k <= res; res -= k, k *= 2) {
        for(int j = m; j >= v[i] * k; j --) 
            f[j] = max(f[j],f[j - v[i] * k] + w[i] * k);
    }
    // 零头次的 01背包
    for(int j = m; j >= v[i] * res; j --)
        f[j] = max(f[j],f[j - v[i] * res] + w[i] * res);
}

分组背包

每组物品只能选择一个

考虑前 i 组物品以后，总体积为 \(0,1,...,m\) 时的最大收益

  • 第 i 组物品一个没取：问题变成了前 \(i - 1\) 组物品，总体积为 \(j\)
  • 第 i 组物品取了，枚举取了其中的物品 k：问题变成了前 i - 1 组物品，总体积为 \(j - v_k\)

核心代码

体积从大到小枚举只能选一个（01背包），体积从小到大枚举可以选多个（完全背包）

int v[N],w[N],a[N],f[N];
vector<int> c[N];

for(int i = 1; i <= n; i ++) {
    cin >> a[i] >> v[i] >> w[i];
    c[a[i]].push_back(i);
}

// 至多有 1000 组
for(int i = 1; i <= 1000; i ++) 
    for(int j = m; j >= 0; j --) {
        // f[i][j] = f[i-1][j];
        for(auto k: c[i])
            if(v[k] <= j) {
                // f[i][j] = max(f[i][j],f[i-1][j - v[k]] + w[k]);
                f[j] = max(f[i][j],f[j - v[k]] + w[k]);
            }
    }
cout << f[m];

二维背包

容量 和 体力 两个维度

如何选择物品，是的在物品的总体积不超过 m 且花费总体力不超过 k 的情况下，获得的最大的收益？

考虑前 \(i\) 个物品，总体积为 \(j\)，总体力为 \(x\) 时

  • 第 \(i\) 个物品没取：问题变成了前 \(i - 1\) 个物品，总体积为 \(j\)，总体力为 \(x\)
  • 第 \(i\) 个物品取了：问题变成了前 \(i - 1\) 个物品，总体积为 \(j - v_i\) ，总体力为 \(x - t _i\)​
int t[N]; // 体力
for(int i = 1; i <= n; i ++)
    for(int j = m; j >= v[i]; j --)
        for(int k = x; x >= w[i]; j --)
            f[j][k] = max(f[j][k],f[j - v[i]][k - t[i]] + w[i]);

cout << f[m][k];

区间dp

石子合并

正着考虑很显然，但是不好得出结论，尝试反着推。

考虑最后合并的两对石子，存在一个分界线 x

  • 其中一堆：第 1 堆石子到第 x 堆石子合并得到的结果
  • 另外一堆：第 x + 1 堆石子到第 n 堆石子合并得到的结果
  • 总代价：左 + 右 + 总石子数

我们不知道分界线 x 在哪里总代价最小，于是我们可以枚举 x 的位置

记忆化搜索

int n,a[N],s[N],f[N][N]; 
// memset(f,255,sizeof(f));  初始化为 -1
// s[N] 为前缀和
int dp(int l,int r) {
    if(f[l][r] != -1) return f[l][r];
    if(l == r) return f[l][r] = 0;

    int res = 1 << 30;
    for(int x = l; x < r; x ++) 
        res = min(res, dp(l,x) + dp(x + 1,r));

    return f[l][r] = res + s[r] - s[l - 1];
}

递推写法

int n,a[N],s[N],f[N][N];
// memset(f,0x3f,sizeof(f));

void solve() {
    for(int i = 1; i <= n; i ++) f[i][i] = 0;

    // i 表示区间长度，j 是左端点，k 是分界线
    for(int i = 1;i < n; i ++) 
        for(int j = 1; j <= n - i; j ++)
            for(int k = j; k < j + i; k ++)
                f[j][j + i] = min(f[j][j + i], 
                            f[j][k] + f[k + 1][j + i] + s[j + i] - s[j - 1]);

    cout << f[1][n];
}

括号序列

令A， B是合法的子序列

  • (A)或[A]： 如果 \(s_i\) 和 \(s_j\) 匹配，f[i][j] = max(f[i][j], f[i + 1][j - 1] + 2);
  • AB： 枚举AB 的分界线 k，f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j]);
char s[N];
int n,f[N][N];

void solove() {
    cin >> n >> s + 1;
    memset(f,0,sizeof(f));

    // i 是长度，j 是左端点，k 是分界线。
    for(int i = 1; i < n; i ++) 
        for(int j = 1; j <= n - i; j ++) {
            if((s[j] == '(' && s[j + i] == ')') ||
                s[j] == '[' && s[j + i] == ']')
                f[j][j + i] = f[j + 1][j + i - 1] + 2;

            for(int k = j; k < j + i; k ++)
                f[j][j + i] = max(f[j][j + i], f[j][k] + f[k + 1][j + i]);
        }

    cout << f[1][n];
}

石子合并（二）

通过倍增的思想，破环成链，然后就是石子合并的区间合并。

int n,a[N],s[N],f[N][N];

void solve()
{
    cin >> n;
    for(int i = 1; i <= n; i ++) {
        cin >> a[i];
        a[n + i] = a[i];
    }
    n += n;
    for(int i = 1; i <= n; i ++) s[i] = s[i-1] + a[i];

    memset(f,0x3f,sizeof(f));

    for(int i = 1; i <= n; i ++) f[i][i] = 0;
    for(int i = 1; i < n; i ++) 
        for(int j = 1; j <= n - i; j ++)
            for(int k = j; k < j + i; k ++)
                f[j][j + i] = min(f[j][j + i],f[j][k] + f[k + 1][j + i] + s[j + i] - s[j - 1]);

    int res = inf;
    for(int i = 1; i <= n/2 ; i ++)
        res = min(res,f[i][i + n/2 - 1]);
    cout << res;

}

树形DP

树形DP，只是用树维护DP，没有说用dfs返回值维护DP

  • 边dfs，边更新状态

统计人数

vector<int> f(n,1);
function<void(int)> dfs = [&](int x) -> void {
    for(auto v: g[x]) {
        dfs(v);
        f[x] += f[v];
    }
};
dfs(0);

没有上司的舞会

考虑第 i 号员工，他有参加和不参加舞会两种情况

  • 参加：则他的直接下属都不参加舞会，只需考虑直接下属不参加舞会的情况
  • 不参加：则他的直接下属有参加和不参加舞会两种情况，找个最大值。
\[ 参加：f[i][1] = a[i] + \sum{f[j][0]} \\ 不参加：\sum {\max(f[j][0],f[j][1])}; \]
vector<vector<ll>> f(n,vector<ll>(2,0));    
function<void(int)> dfs = [&](int x) -> void {
    f[x][1] = a[x];
    for(auto v: g[x]) {
        dfs(v);
        f[x][0] += max(f[v][0],f[v][1]);
        f[x][1] += f[v][0];
    }
};
dfs(0);

cout << max(f[0][0],f[0][1]);

新的背包

转移：枚举第 \(i\) 种物品取了 \(k\) 个，从中选择收益最大的方案 $$ f[i][j] = \max_{0\le k \le j}(f[i-1][j-k] + w[i][k]) $$

// 01 背包
vector<int> f(m + 1,0);
for(int i = 0; i < n; i ++)
    for(int j = m; j >= 0; j --)
    {
        // 有 k 中选择，k 个物品的价值是 w[i][k-1]
        for(int k = 1; k <= j; k ++) 
            f[j] = max(f[j],f[j - k] + w[i][k-1]); 
    }

cout << f[m];

没有上司的舞会（二）

多了人数的限制，是 没有上司的舞会 和 新的背包 组合体。

加一维度考虑：用 f[i][j][0],f[i][j][1] 分别表示考虑第 \(i\) 号员工的团队，团队中一共有不超过 \(j\) 个人，他参加或不参加的最大快乐值。

int f[501][501][2]{0};
function<void(int)> dfs = [&](int x) -> void {
    for(auto& y: g[x]) {
        dfs(y);
        for(int j = m; j >= 0; j --) {

            // k 中选择
            for(int k = 1; k <= j; k ++) {
                f[x][j][0] = max(f[x][j][0], f[x][j - k][0] + max(f[y][k][0], f[y][k][1]));
                f[x][j][1] = max(f[x][j][1], f[x][j - k][1] + f[y][k][0]);
            }
        }
    }
    // 加上 x 的快乐值
    for(int j = m; j >= 1; j --) f[x][j][1] = f[x][j-1][1] + a[x];
    f[x][0][1] = 0;
};

换根DP

距离和

求出每个点到其他所有点的距离和

size[i]：表示以 \(i\) 为根的子树有多少点

f[i]：表示以 \(i\) 为根的子树，\(i\) 到其他所有点的距离和

  • 假设 \(j\) 是 \(i\) 的儿子，则 f[i] += f[j] + size[j]

  • 到点 \(i\) 的距离比到点 \(j\) 的距离多 \(1\), 有 \(size[j]\) 个点，所以多 \(size[j]\) 的距离

  • 所以：\(f[i] = size[i] - 1 + \sum_{j \in son(i)} {f[j]}\)

Last update: January 5, 2025
Created: February 14, 2024

Comments