01 预备知识¶
约 1451 个字 15 行代码 预计阅读时间 5 分钟
tensor¶
张量:tensor
shape属性:张量的形状numel属性:张量中元素的总数reshape:改变张量形状-
cat:把两个张量连结在一起- 指定按那个维度连结:如 dim = 0(行),dim = 1(列)
-
sum:对张量中所有元素求和 - 广播机制
- 两个形状不同的张量做运算
- 维度为 1 的数组进行复制,使得达到相同的维度
- 然后再做运算
- \(1 * 3\) 矩阵和 \(2 * 1\) 矩阵相加,得到 \(2 * 3\) 矩阵
学点英语单词
numel: It refers to the “number of elements” in an array or matrix.
索引和切片¶
第一个元素的索引是 \(0\),最后一个元素索引是 \(-1\);
切片是 左闭右开 的
X[1:3]第一行和第二行的元素 (0 base)
赋值:X[1,2] = 9
数据预处理¶
处理缺失值
- 插值法
- 删除法
学点英语单词
iloc: index location
NaN:not a number
线性代数¶
矩阵范数¶
矩阵范数(Matrix Norm)是用于量化矩阵大小的一种度量方式,类似于向量范数对向量大小的度量。
范数就是表示矩阵的长度。
Frobenius 范数:
轴¶
axis:轴/维度
考虑一个形状为 (2, 3, 4) 的三维数组 array_3d:
import numpy as np
array_3d = np.array([[[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]],
[[13, 14, 15, 16],
[17, 18, 19, 20],
[21, 22, 23, 24]]])
这个数组可以理解为两个 3x4 的二维数组叠加在一起:
array_3d[0] = [[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]]
array_3d[1] = [[13, 14, 15, 16],
[17, 18, 19, 20],
[21, 22, 23, 24]]
- 按 axis = 0 分开:
array_3d[0,:,:]和array_3d[1,:,:]] - 按 axis = 1 分开:把上面的两个二维数组的下一维度(行)拿出来
array_3d[0,0,:]和array_3d[0,1,:]和array_3d[0,2,:]array_3d[1,0,:]和array_3d[1,1,:]和array_3d[1,2,:]
- 按 axis = 2 分开:把上面的六个行向量的下一维度(列)拿出来 (具体到这个例子来说,就是把每个元素拿出来)
array_3d[0][0][0]和array_3d[0][0][1]和array_3d[0][0][2]和array_3d[0][0][3]array_3d[0][1][0]和array_3d[0][1][1]和array_3d[0][1][2]和array_3d[0][1][3]- ...
array_3d[1][2][0]和array_3d[1][2][1]和array_3d[1][2][2]和array_3d[1][2][3]
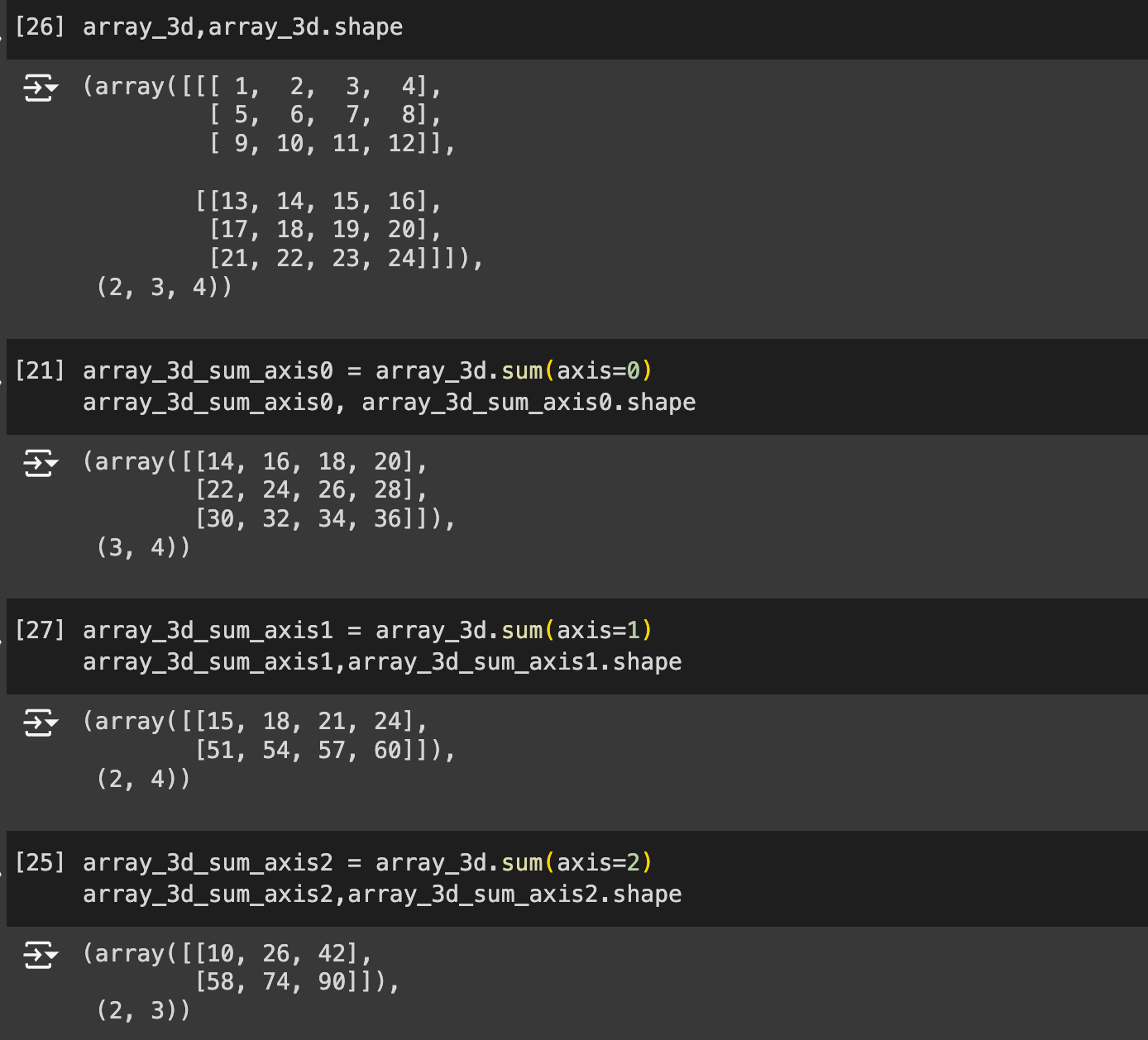
代码示例
array_3d_sum_axis1 = array_3d.sum(axis=1)
array_3d_sum_axis1,array_3d_sum_axis1.shape
# (array([[15, 18, 21, 24],
# [51, 54, 57, 60]]),
# (2, 4))
按 axis = 1 分开:把上面的两个二维数组的下一维度(行)拿出来
array_3d[0,0,:]和array_3d[0,1,:]和array_3d[0,2,:]求和得:[15, 18, 21, 24]array_3d[1,0,:]和array_3d[1,1,:]和array_3d[1,2,:]求和得:[51, 54, 57, 60]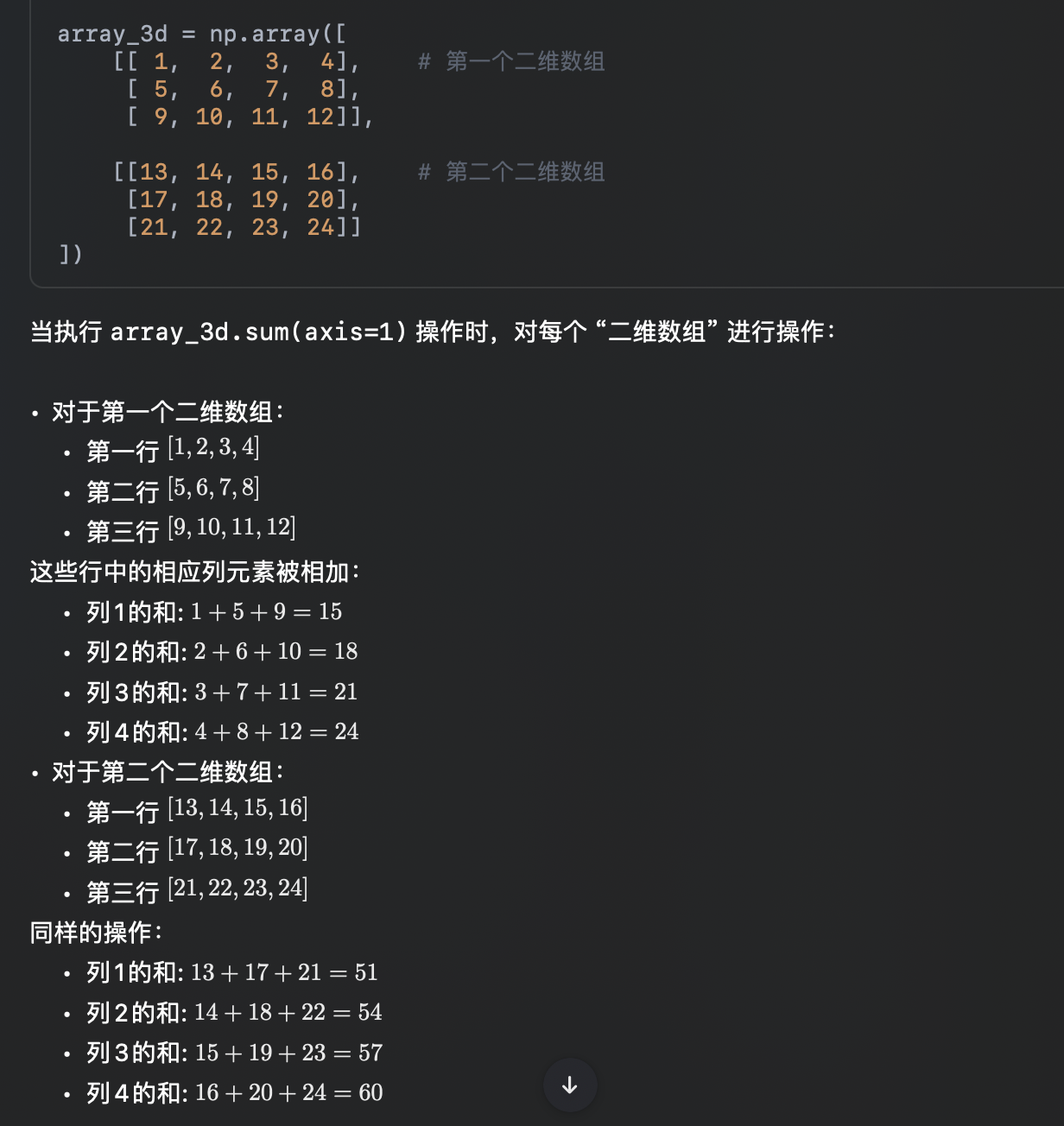
指定 axis=1 将通过汇总每个二维数组中所有行的元素来降维。因此,在输出形状中,原输入的 axis=1(行的维度)将不再存在。
从而将原始三维数组沿 axis=1(行)压缩为一个二维数组。
矩阵计算¶
分子布局还是分母布局是无所谓的。
标量对向量求导

向量对标量求导

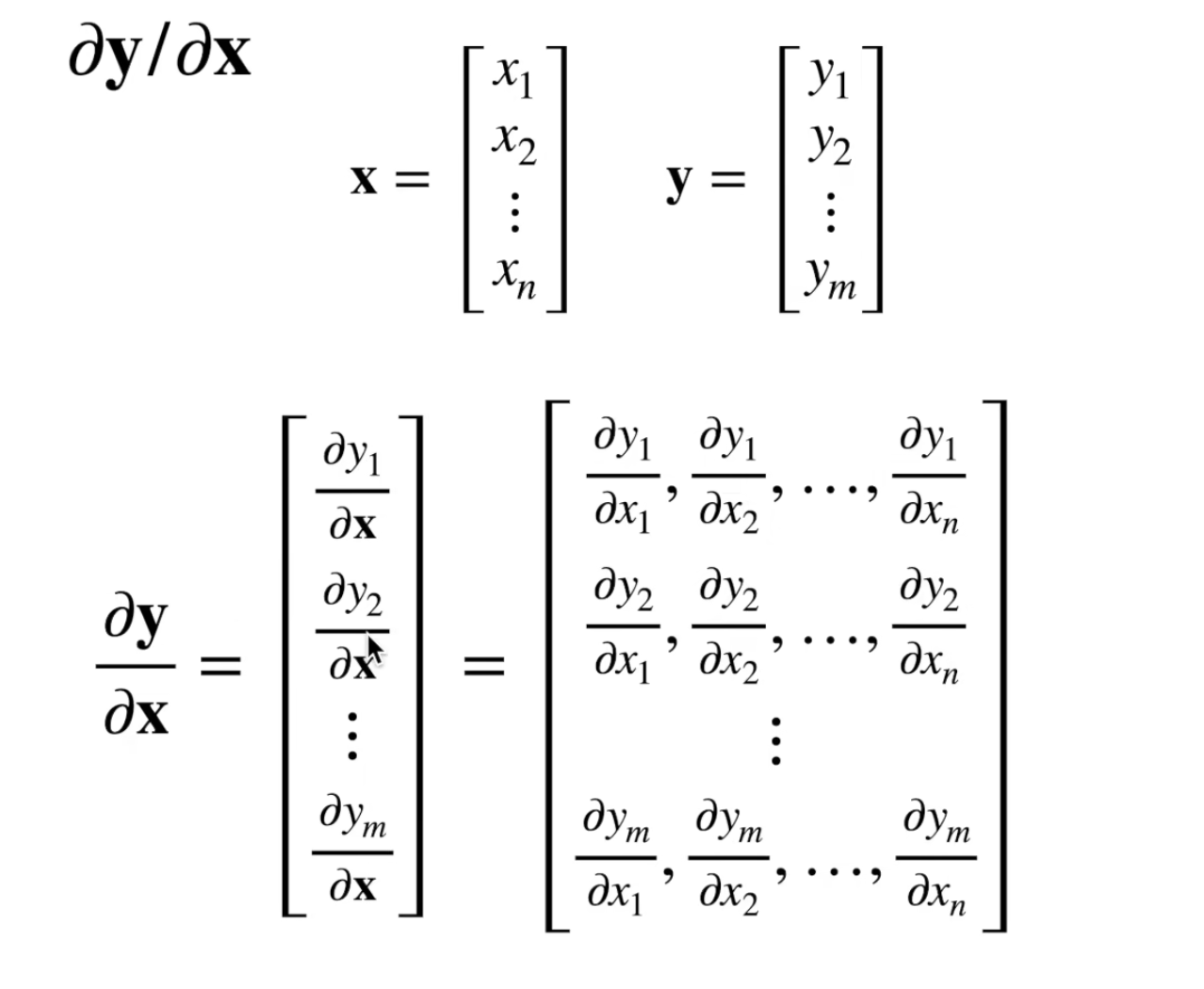
向量对向量求导
常用公式¶

其中 \(I\) 是单位矩阵(Identity Matrix)
\(A\) 和 \(\vec{x}\) 做内积,对 \(\vec{x}\) 的偏导为 \(A^T\)。公式如下
扩展到矩阵¶

矩阵 \(\mathbf{X}\) 是一个二维数组,可以表示为: \(\mathbf{X} \in \mathbb{R}^{n \times k}\)
如果 \(y\) 是一个标量,对矩阵 \(\mathbf{x}\) 的导数为:\(\frac{\partial y}{\partial \mathbf{X}} \in \mathbb{R}^{k \times n}\)
如果 \(y\) 是一个向量 \((m,1)\),对矩阵 \(\mathbf{x}\) 的导数为:\(\frac{\partial \mathbf{y}}{\partial \mathbf{X}} \in \mathbb{R}^{m \times k \times n}\)
- 拆分 \(y\) 的每个列,当做是一个标量
如果 \(y\) 是一个矩阵 \((m,l)\),对矩阵 \(\mathbf{x}\) 的导数为:\(\frac{\partial \mathbf{Y}}{\partial \mathbf{X}} \in \mathbb{R}^{m \times l \times k \times n}\)
- 矩阵的每个元素 \(y_{ij}\) 都要计算。
学点新知识
自动求导¶
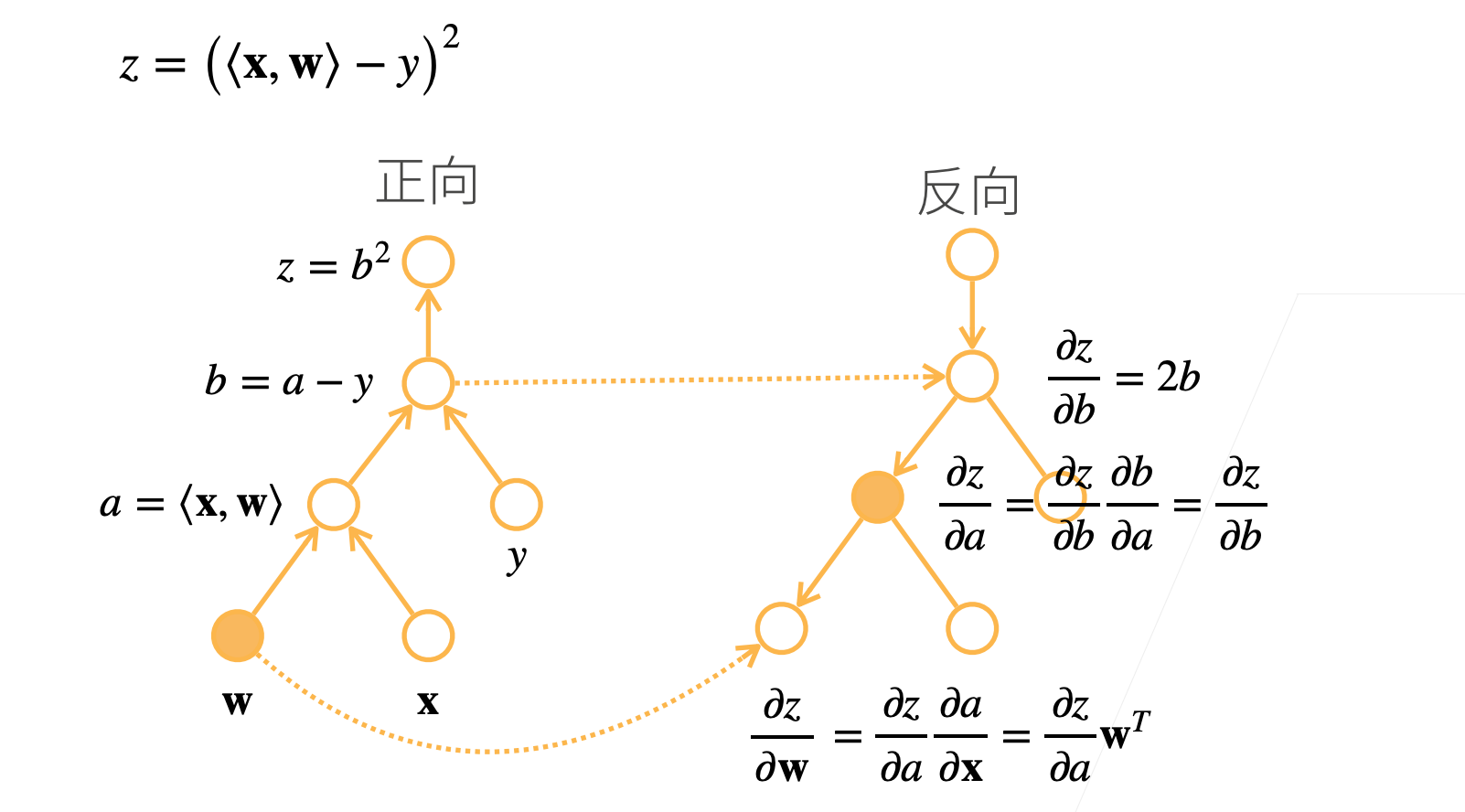
构造计算图
- 前向:执行图,存储中间结果
- 反向:从相反方向执行图(去除不需要的枝,因为正向已经计算过了)
- 前向计算其实是一个符号求解的的过程,其中每一步的计算都基于前一步的输出。
- 反向计算其实是一个具体数值的求解,即实际的梯度值,这些梯度指导了参数的更新。
numpy 和 pandas¶
在深度学习项目中,numpy 和 pandas 是两个非常重要的库,它们提供了大量的功能来处理和分析数据。这里为您列举一些在深度学习中常用的 numpy 和 pandas 方法或函数:
Numpy 方法¶
numpy.array()- 创建数组。numpy.dot()- 矩阵乘法,用于前向和反向传播中的加权和。numpy.exp()- 指数函数,常用于激活函数如 softmax 的计算。numpy.log()- 对数函数,常用于计算损失函数,如交叉熵损失。numpy.mean()- 计算平均值,常用于批量数据处理。numpy.std()- 计算标准差,用于数据标准化。numpy.sum()- 计算元素总和,常用于某一维度的求和操作。numpy.max()- 计算最大值,有时用于激活函数如 ReLU。numpy.min()- 计算最小值。numpy.reshape()- 改变数组的形状,常用于调整输入数据的维度。numpy.transpose()- 矩阵转置,有时用于调整矩阵的维度。
Pandas 方法¶
pandas.read_csv()- 从 CSV 文件加载数据,常用于读取数据集。pandas.DataFrame()- 创建 DataFrame 对象,方便数据操作和分析。DataFrame.head()- 查看 DataFrame 的前几行数据,用于快速检查数据或调试。DataFrame.describe()- 提供数据的统计摘要,包括均值、标准差、最小值、最大值等。DataFrame.drop()- 删除表中的不需要的列或行。DataFrame.iloc[]- 基于整数位置的索引,选择数据。DataFrame.loc[]- 基于标签的索引,选择数据。DataFrame.groupby()- 对数据进行分组,常用于计算分组统计。DataFrame.merge()- 合并两个 DataFrame,常用于结合来自不同数据源的数据。DataFrame.fillna()- 填充 NA/NaN 值,用于处理缺失数据。
Created: August 2, 2024